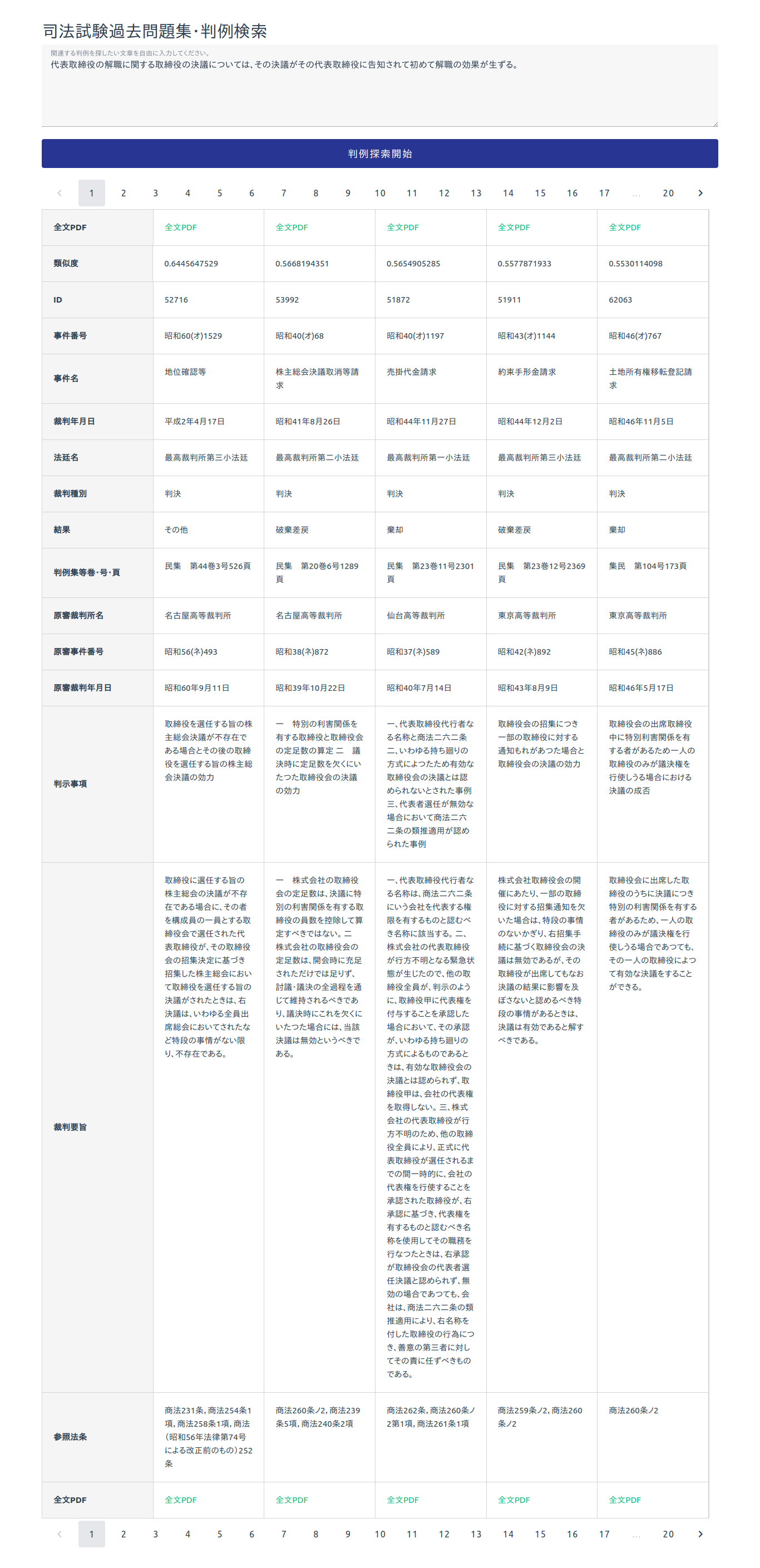
記事タイトルの通りです。
AWSのLightsailにはDjangoの設計図(テンプレート)が用意されているので簡単に公開できるのかなと思っていたのですが、意外と苦労しました。
そのための手順を説明した記事やドキュメントも不足気味です。
そこでこの記事にまとめました。
1.前提
ローカル環境でDjangoのプロジェクトの開発をして、GitHubで管理していることを前提とします。
GitHubのリポジトリの中にrequirements.txtファイルやmanage.pyファイルとDjangoのプロジェクトディレクトリがあり、Djangoのプロジェクトディレクトリの中にsettings.pyファイルがあると想定します。
ウェブサーバーはApache、データベースはMariaDB(MySQL)とします。
AWSのアカウントは設定済みとします。
2.インスタンスを作成する
インスタンスの作成は簡単です。
Lightsailからインスタンスを作成する画面で、設計図のところからDjangoを選ぶだけで、その他はデフォルトのままでよいです。
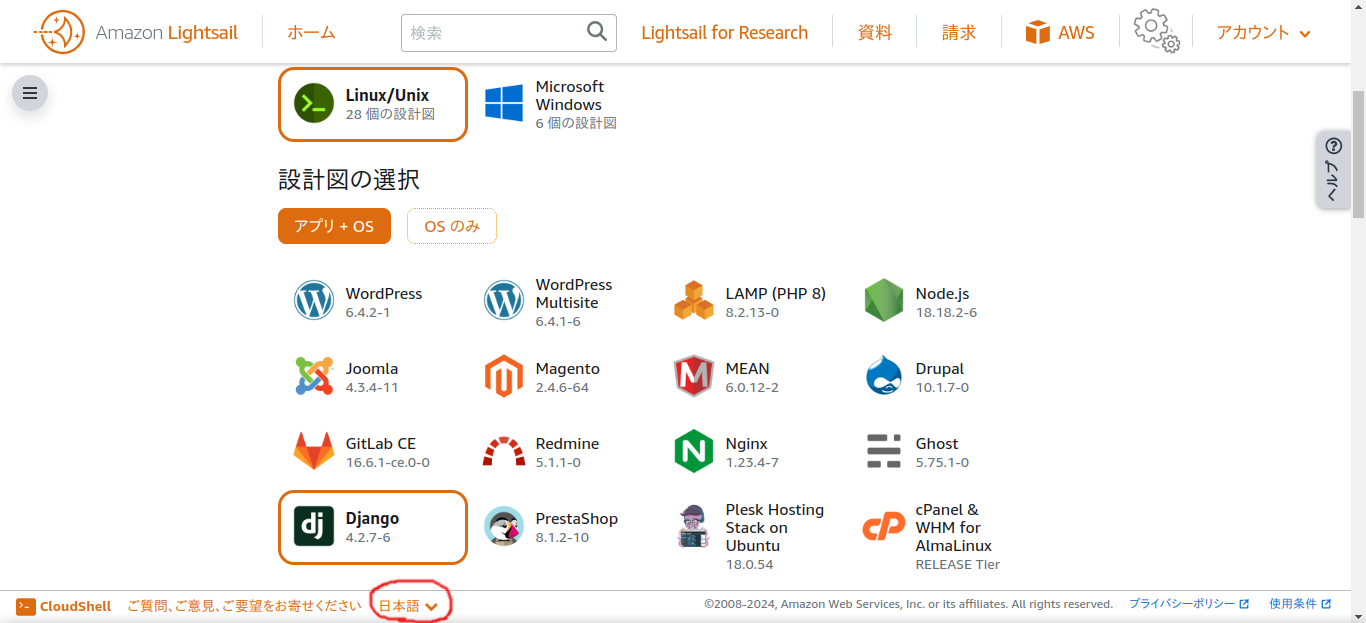
必要なら適当に変更してください。
表示言語設定は画面下部の赤丸で囲んだところにあるので、日本語がよければここから日本語に変更してください。
3.インスタンスに接続する
ターミナルのようなアイコンをクリックするか、縦に3つの点が並んでいるアイコンをクリックして「接続」を選ぶかして、ブラウザベースのSSHクライアントを立ち上げます。
黒い背景にコマンドを打ち込むターミナル画面が起動すれば成功です。
インスタンスを作成してから数分経過しないとうまく立ち上がらないです。
簡単さのためにこの記事ではブラウザベースのSSHクライアントを利用しますが、お使いのマシンからSSH接続しても構いません。
4.GitHubからリポジトリをクローンする
(1) リポジトリをクローンするためのディレクトリを作成する
どこでリポジトリをクローンしてもよいのですが、Bitnamiの公式チュートリアルのGet started with Djangoに従って配置したほうがわかりやすいです。
sudo mkdir /opt/bitnami/projects
sudo chown -R $USER /opt/bitnami/projects
コマンドの貼り付けは、右クリックからするようにしてください。
(2) GitHubのアカウントにSSHキーを追加する
秘密鍵と公開鍵を作成し、公開鍵をGitHubのアカウントに追加します。
秘密鍵と公開鍵を作成するコマンドは以下です。
いくつか質問をされますが、デフォルトのままエンターキーを押していけばよいでしょう。
次に、作成した公開鍵を表示します。
cat /home/bitnami/.ssh/id_rsa.pub
ssh-rsaから始まってbitnami@ip-172-26-9-251のような文字列で終わる暗号のような文字が表示されるはずですから、この全体を右クリックからコピーします。
それを以下のようなGitHubのSSHキー追加画面に貼り付けて追加します。
titleの部分は何でもよいです。
(3) GitHubからリポジトリをクローンする
これでGitHubからリポジトリをクローンできるはずです。
cd /opt/bitnami/projects/
git clone git@github.com:GITHUBACCOUNT/GITHUBREPOSITORY.git
GITHUBACCOUNTとGITHUBREPOSITORYの部分は、ご自身のリポジトリに合わせてください。
初回の接続なので接続するかどうかを尋ねられますが、「yes」と入力してエンターキーを押してください。
5.pipコマンドでPythonのパッケージをインストールする
GitHubのリポジトリ直下に用意したrequirements.txtファイルを利用して必要なPythonのパッケージをインストールします。
cd /opt/bitnami/projects/GITHUBREPOSITORY
sudo pip install -r requirements.txt
GITHUBREPOSITORYは先ほどクローンしたGitHubのリポジトリ名です。
mysqlclientのインストールに失敗するはずなので、mysqlclient · PyPIに載っている以下のコマンドを実行してから再挑戦します。
sudo apt-get install python3-dev default-libmysqlclient-dev build-essential pkg-config
sudo pip install -r requirements.txt
インストールの確認を求められたら、yと入力してエンターキーを押してください。
Lightsail自体が仮想環境なのですから、Pythonの仮想環境を作成せず、sudoでpipを実行してインストールしています。
これが一番簡単です。
6.データベースを作成する
MariaDB(MySQL)が最初からインストールされてはいるのですが、Djangoで使うためのデータベースを自分で作成しなければなりません。
データベースに接続するためのパスワードがわからなくて私はハマりました。
ホームディレクトリのbitnami_application_passwordに書いてあるのですね。
ということでまずそのパスワードを表示します。
cat /home/bitnami/bitnami_application_password
パスワードが表示されたことを確認してから、次のコマンドを実行します。
パスワードの入力を求められるので、先ほど表示させたパスワードを右クリックからコピーし、右クリックで貼り付け、エンターキーを押します。
MariaDBに入ることができたら、以下のコマンドを実行して、データベースを作成します。
CREATE DATABASE XXXXXXXX;
XXXXXXXXの部分には、Djangoのプロジェクト名など、適当なデータベース名を指定してください。
データベースを無事に作成できたら以下のコマンドを実行してMariaDBから抜けます。
7.Djangoの設定をする
(1) settings.pyを調整する
Get started with Djangoを参考にしてsettings.pyを調整します。
データベース接続の部分は以下のように設定します。
DATABASES = {
'default': {
'ENGINE': 'django.db.backends.mysql',
'NAME': 'XXXXXXXX',
'HOST': '/opt/bitnami/mariadb/tmp/mysql.sock',
'PORT': '3306',
'USER': 'root',
'PASSWORD': 'PASSWORD'
}
}
XXXXXXXXの部分は、先ほど作成したデータベース名にします。
PASSWORDの部分は、bitnami_application_passwordに書いてあるパスワードにします。
ALLOWED_HOSTSの部分は、接続確認を優先して、ひとまず*に設定します。
接続確認できたらドメイン名に設定し直してください。そのときにDEBUGもfalseにしてください。
Lightsailに配置すべきsettings.pyファイル全体をローカル環境のエディタで記載し、それをコピーして貼り付けるようにするのが簡単かなと思います。
まずsettings.pyファイルが存在しているかを確認します。
cat /opt/bitnami/projects/GITHUBREPOSITRY/DJANGOPROJECT/settings.py
GITHUBREPOSITRYは先ほどクローンしたGitHubのリポジトリ名、DJANGOPROJECTはそのリポジトリ直下にあるはずのDjangoのプロジェクト名です。これらは同じ名前にすることが一般的ですが、異なる名前でも構いません。
settings.pyファイルの存在確認ができたら、それをviで開いて、内容をいったん全部削除し、ローカル環境からコピーした内容を貼り付けます。
vi /opt/bitnami/projects/GITHUBREPOSITRY/DJANGOPROJECT/settings.py
viでsettings.pyファイルを開きますので、以下のコマンドを入力してエンターキーを押して内容をいったん全部削除します。
ローカル環境のエディタで作成したsettings.pyファイルの内容を全部コピーして、右クリックから貼り付けます。
そうするとviの入力モードになっていますから、Ctrl+Cを押してコマンドモードに移行し(Escではコマンドモードに移行できませんでした)、次のコマンドを実行して保存して終了します。
ここでは簡便さのために直接settings.pyファイルを編集しましたが、できれば.envファイルで設定するほうがよいです。
(2) データベースにmigrateする
ここからはLightsail特有の手順ではなくDjangoの標準的な手順です。
python /opt/bitnami/projects/DJANGOPROJECT/manage.py migrate
このようなコマンドでmigrateします。
上記は絶対パスで記載しましたが、DJANGOPROJECTディレクトリの中にいるなら以下のコマンドで実行できます。
(3) 静的ファイルをcollectstaticで集める
これもmigrateと同じ要領です。
python /opt/bitnami/projects/DJANGOPROJECT/manage.py collectstatic
または
python manage.py collectstatic
8.Apacheの設定をする
本来であれば、ここでmanage.pyのrunserverを実行して確認するとよいのでしょうが、そのためにはファイアウォールの設定を追加するなどの手間が生じますので、いきなりウェブサーバーであるApacheの設定をします。
基本的にはDeploy a Django projectに書いてある手順に従います。
sudo cp /opt/bitnami/apache/conf/vhosts/sample-vhost.conf.disabled /opt/bitnami/apache/conf/vhosts/sample-vhost.conf
sudo cp /opt/bitnami/apache/conf/vhosts/sample-https-vhost.conf.disabled /opt/bitnami/apache/conf/vhosts/sample-https-vhost.conf
コピーしたApacheの設定ファイル中のsampleをGITHUBREPOSITORYとDJANGOPROJECTに置換します。
GITHUBREPOSITORYとDJANGOPROJECTが同じ名前なら、以下のコマンドだけで置換できます。
sed -i s/sample/GITHUBREPOSITORY/g /opt/bitnami/apache/conf/vhosts/sample-vhost.conf
sed -i s/sample/GITHUBREPOSITORY/g /opt/bitnami/apache/conf/vhosts/sample-https-vhost.conf
GITHUBREPOSITORYとDJANGOPROJECTが異なる名前なら、以下のように2段階で置換します。
sed -i s/sample/GITHUBREPOSITORY/g /opt/bitnami/apache/conf/vhosts/sample-vhost.conf
sed -i s@GITHUBREPOSITORY/GITHUBREPOSITORY@GITHUBREPOSITORY/DJANGOPROJECT@g /opt/bitnami/apache/conf/vhosts/sample-vhost.conf
sed -i s/sample/GITHUBREPOSITORY/g /opt/bitnami/apache/conf/vhosts/sample-https-vhost.conf
sed -i s@GITHUBREPOSITORY/GITHUBREPOSITORY@GITHUBREPOSITORY/DJANGOPROJECT@g /opt/bitnami/apache/conf/vhosts/sample-httpsvhost.conf
最後にApacheを再起動します。
sudo /opt/bitnami/ctlscript.sh restart apache
9.ネットワークの設定をする
ブラウザでインスタンスを作成したページに戻り、「Django-1」のようなインスタンスの名前をクリックして、「ネットワーキング」というタブから、静的IPをアタッチします。
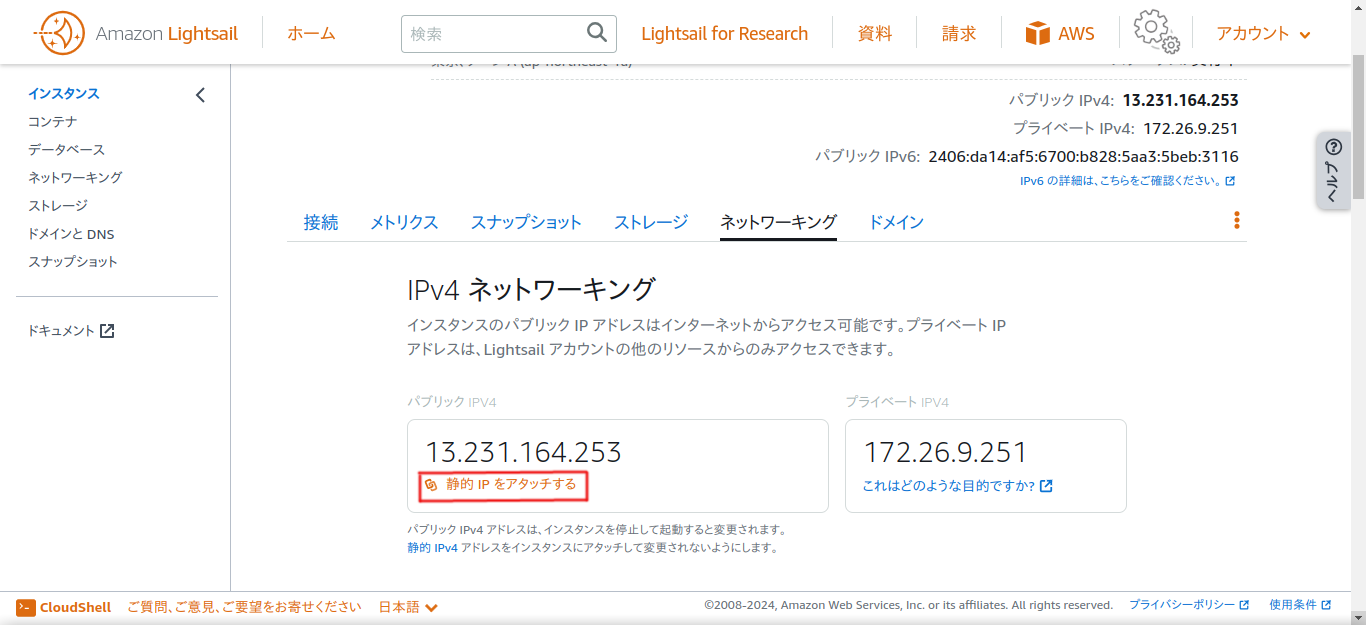
そこに表示されているパブリックIPV4アドレスの数字をブラウザのURL欄に打ち込むと、ページが表示されるはずです。
httpsではないためにブラウザが警告を発することがありますが、危険性を承知の上で続行するとページが表示されます。
10.HTTPSの設定をする
独自ドメインのAレコードに先ほど接続確認をしたパブリックIPV4アドレスの数字を設定してからの作業になります。
Auto-configure a Let’s Encrypt certificateに書いてある手順そのままです。
sudo /opt/bitnami/bncert-tool
リダイレクトの設定やメールアドレスなどを質問されるので、適当に答えてください。
11.ハマりやすいポイント
(1) ブラウザベースのSSHクライアント
ブラウザベースのSSHクライアントのコピーアンドペーストに少しハマりました。
結論としては、すべて右クリックで操作することです。
SSH接続のための公開鍵のコピーをコマンドでしようとしたら失敗しました。
また、viもEscキーでコマンドモードに戻れないなど、いつもの操作と挙動が異なり戸惑いました。
日本語が表示されず文字化けすることにも苦しめられました。
環境変数の変更などを試してみてもうまくいきませんでした。
文字化けしている部分をコピーしてSSHクライアント以外の場所に貼り付けると読めるようになるので、それで一時しのぎはできます。
(2) Pythonのパッケージ管理
結論としては、上記に記載したように、/opt/bitnami/projects/以下にDjangoのファイルを配置して、sudo pipでパッケージをインストールすることになります。
最初はホームディレクトリにDjangoのファイルを配置したせいで、wsgi.pyファイルで no module named DJANGOPROJECT(DJANGOPROJECTは具体的なプロジェクトの名前)エラーが発生してハマりました。
/opt/bitnami/apache/logs/error_logのApacheのエラーログを見てこのエラーに気づきました。
そのときはwsgi.pyファイルに以下の記述を追加して一時的に切り抜けました。
import sys
sys.path.append(os.path.dirname(os.path.abspath(__file__)))
sys.path.append(os.path.dirname(os.path.abspath(__file__)) + '/..')
この記事の上の部分で説明したように公式ドキュメントに準拠した場所に配置すれば、このような一時しのぎは不要です。
(3) mysqlclientのインストールエラー
これも記事中に記載した通りです。
公式ドキュメントをきちんと読まなければなりませんね。