scikit-learnでMNIST手書き数字の分類機械学習 – 浅野直樹の学習日記の続きです。
今回はモデルやパラメータの選択に挑戦してみます。
その前に、次元削減、パイプライン、交差検証の練習をしておきます。
1.次元削減
今回は学習を何度も実行するので、その学習にかかる時間を短くできるように特徴量の次元削減をします。
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.decomposition import PCA
#データの読み込み
digits = datasets.load_digits()
#PCAによって削減される特徴量数と失われるデータの分散との関係を表示
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')以下のような図が表示されます。
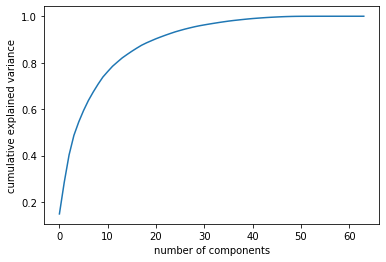
コードはIn Depth: Principal Component Analysis | Python Data Science Handbookから流用させてもらいました。
この図を見ると、元のデータの分散の0.95を説明できるようにしても特徴量の数を半分以下にできそうです。
実際に試してみましょう。
#PCAで次元削減
pca = PCA(0.95).fit(digits.data)
reduced_data = pca.transform(digits.data)
restored_data = pca.inverse_transform(reduced_data)
print('pca.n_components_:', pca.n_components_)
print('digits.data.shape:', digits.data.shape)
print('reduced_data.shape:', reduced_data.shape)
print('restored_data.shape:', restored_data.shape)
####次元削減をしてから元に戻した手書き数字データの画像表示####
#描画領域の確保
fig, axes = plt.subplots(10, 10, figsize=(15, 15), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.5, wspace=0.5))
#最初の100枚の確保した描画領域に表示
for i, ax in enumerate(axes.flat):
ax.imshow(restored_data[i].reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest')
ax.set_title(digits.target[i])次のような文字列と画像が出力されます。
pca.n_components_: 29
digits.data.shape: (1797, 64)
reduced_data.shape: (1797, 29)
restored_data.shape: (1797, 64)
特徴量の次元数を64から29に減少させたたのに、画像を目視で確認すると次元削減をしなかった前回と比べても変化に気づかないくらいです。
なお、ここで言っている次元数は特徴量の次元数のことであって、配列の次元数ではないことにご注意ください。機械学習をするための配列の次元数は常に2です。
2.パイプライン
これから特徴量の次元数を削減してからいろいろなモデルで学習させることになるので、特徴量の次元削減とモデルとをパイプラインでくっつけます。
最初に一度だけデータ全体の特徴量の次元削減をしてからいろいろなモデルで学習させればよいのではないかと思う人もいるかもしれませんが、次元削減は訓練データにだけするようにしないと情報がリークして学習に悪影響を及ぼしてしまうので、そうしてはいけません。
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.pipeline import Pipeline
from sklearn.metrics import accuracy_score
#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, shuffle=False)
#パイプラインの構築
steps = [('pca', PCA()), ('model', svm.SVC())]
pipe = Pipeline(steps)
#構築したパイプラインで学習
pipe.fit(X_train, y_train)
#学習結果のテスト
y_model = pipe.predict(X_test)
accuracy_score(y_test, y_model)結果は以下です。
0.9622222222222222前回と似たような値になりました。
3.交差検証
これまでは1回のテストでスコア(正解率)を計算してきましたが、訓練データとテストデータの分け方によってその値が変わります。
そこで、交差検証を導入して複数回のテストを行い、より信頼できる値を出してみます。
from sklearn.model_selection import cross_val_score
#交差検証
scores = cross_val_score(pipe, digits.data, digits.target, cv=3)
print('scores:', scores)
print('average_score:', scores.mean())出力は以下です。
scores: [0.96994992 0.98330551 0.96994992]
average_score: 0.9744017807456872scikit-learnのおかげで簡単にできました。
4.モデル選択
いよいよ本題のモデル選択です。scikit-learnには全てのモデルを返してくれるall_estimators()関数があるのでこれを使いましょう。
もう一度データの読み込みからやり直して一気に行きます。
import warnings
import pandas as pd
from sklearn import datasets
from sklearn.utils import all_estimators
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
from sklearn.model_selection import cross_val_score
#警告の非表示
warnings.filterwarnings('ignore')
#結果を格納するデータフレームの作成
df = pd.DataFrame(columns=['model_name', 'score1', 'score2', 'score3', 'average_score'])
#データの読み込み
digits = datasets.load_digits()
#全てのモデルで学習
for (name, algorithm) in all_estimators(type_filter="classifier"):
try:
steps = [('pca', PCA()), ('model', algorithm())]
pipe = Pipeline(steps)
scores = cross_val_score(pipe, digits.data, digits.target, cv=3)
df.loc[len(df)+1] = [name, *scores, scores.mean()]
except:
pass
#スコアのいい順に並べ替えて表示
sorted_df = df.sort_values('average_score', ascending=False)
sorted_df.set_axis(range(1, (len(df)+1) ), axis='index')気になる結果を表示します。
| model_name | score1 | score2 | score3 | average_score | |
|---|---|---|---|---|---|
| 1 | SVC | 0.969950 | 0.983306 | 0.969950 | 0.974402 |
| 2 | KNeighborsClassifier | 0.958264 | 0.963272 | 0.966611 | 0.962716 |
| 3 | ExtraTreesClassifier | 0.949917 | 0.956594 | 0.943239 | 0.949917 |
| 4 | NuSVC | 0.943239 | 0.956594 | 0.936561 | 0.945465 |
| 5 | MLPClassifier | 0.921536 | 0.951586 | 0.933222 | 0.935448 |
| 6 | LogisticRegressionCV | 0.923205 | 0.951586 | 0.928214 | 0.934335 |
| 7 | RandomForestClassifier | 0.924875 | 0.929883 | 0.933222 | 0.929327 |
| 8 | LogisticRegression | 0.924875 | 0.934891 | 0.923205 | 0.927657 |
| 9 | SGDClassifier | 0.918197 | 0.934891 | 0.901503 | 0.918197 |
| 10 | CalibratedClassifierCV | 0.914858 | 0.934891 | 0.903172 | 0.917641 |
| 11 | HistGradientBoostingClassifier | 0.911519 | 0.928214 | 0.908180 | 0.915971 |
| 12 | LinearDiscriminantAnalysis | 0.926544 | 0.911519 | 0.906511 | 0.914858 |
| 13 | PassiveAggressiveClassifier | 0.899833 | 0.934891 | 0.903172 | 0.912632 |
| 14 | LinearSVC | 0.903172 | 0.929883 | 0.888147 | 0.907067 |
| 15 | RidgeClassifierCV | 0.921536 | 0.911519 | 0.879800 | 0.904285 |
| 16 | RidgeClassifier | 0.923205 | 0.906511 | 0.879800 | 0.903172 |
| 17 | GradientBoostingClassifier | 0.898164 | 0.881469 | 0.906511 | 0.895381 |
| 18 | NearestCentroid | 0.891486 | 0.881469 | 0.881469 | 0.884808 |
| 19 | BaggingClassifier | 0.894825 | 0.871452 | 0.846411 | 0.870896 |
| 20 | GaussianNB | 0.881469 | 0.851419 | 0.863105 | 0.865331 |
| 21 | Perceptron | 0.869783 | 0.874791 | 0.789649 | 0.844741 |
| 22 | QuadraticDiscriminantAnalysis | 0.881469 | 0.816361 | 0.813022 | 0.836950 |
| 23 | DecisionTreeClassifier | 0.833055 | 0.766277 | 0.756260 | 0.785198 |
| 24 | BernoulliNB | 0.757930 | 0.777963 | 0.786311 | 0.774068 |
| 25 | ExtraTreeClassifier | 0.621035 | 0.535893 | 0.580968 | 0.579299 |
| 26 | AdaBoostClassifier | 0.292154 | 0.345576 | 0.230384 | 0.289371 |
| 27 | GaussianProcessClassifier | 0.100167 | 0.101836 | 0.101836 | 0.101280 |
| 28 | LabelPropagation | 0.100167 | 0.098497 | 0.098497 | 0.099054 |
| 29 | LabelSpreading | 0.100167 | 0.098497 | 0.098497 | 0.099054 |
| 30 | DummyClassifier | 0.091820 | 0.088481 | 0.091820 | 0.090707 |
| 31 | CategoricalNB | NaN | NaN | NaN | NaN |
| 32 | ComplementNB | NaN | NaN | NaN | NaN |
| 33 | MultinomialNB | NaN | NaN | NaN | NaN |
うまく表示されました。
このようにランキング形式で表示させるのに苦労しました。pandasを使ういい練習になりました。
jupyter notebook上には先ほどのコードを実行するだけで結果がきれいに表示されますが、このブログ記事に載せるためにはto_html()メソッドを使ってhtmlにしました。
all_estimators()関数で取得できるモデルの中にはエラーが発生するものもあるのでtry節の中に入れています。
エラーまでは発生しなくても警告が表示されるものもたくさんあるので警告の表示をしないようにもしました。
本来はこのようにしてテストデータを見てしまうのではなく、Choosing the right estimator — scikit-learn 0.24.2 documentationなどを参考にしながらモデルを選ぶべきなのでしょう。
5.グリッドサーチで最適なパラメータの選択
次は一番成績のよいモデルだったSVCの最適なパラメータを探りましょう。
グリッドサーチで交差検証をしてくれるGridSearchCVに頼ります。
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
import seaborn as sns
#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, shuffle=False)
#パイプラインの構築
steps = [('pca', PCA()), ('model', svm.SVC())]
pipe = Pipeline(steps)
#グリッドサーチのパラメータの設定
param_grid = {
'model__C': [0.1, 1, 10, 100, 1000],
'model__gamma': [0.00001, 0.0001, 0.001, 0.01, 0.1]
}
#グリッドサーチの実行
grid_search = GridSearchCV(pipe, param_grid, cv=3)
grid_search.fit(X_train, y_train)
#結果の表示
print('cv_score:', grid_search.best_score_)
print('best parameters:', grid_search.best_params_)
#テストデータへの適用と結果の表示
y_best_model = grid_search.predict(X_test)
print('test_score:', accuracy_score(y_test, y_best_model))
#結果の可視化
cv_result = pd.DataFrame(grid_search.cv_results_)
cv_result = cv_result[['param_model__gamma', 'param_model__C', 'mean_test_score']]
cv_result_pivot = cv_result.pivot_table('mean_test_score', 'param_model__gamma', 'param_model__C')
heat_map = sns.heatmap(cv_result_pivot, cmap='viridis', annot=True)結果は以下の通りです。
cv_score: 0.96362286562732
best parameters: {'model__C': 10, 'model__gamma': 0.001}
test_score: 0.9688888888888889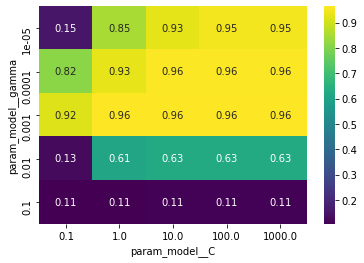
このあたりはAndreas C.Müller, Sarah Guido 著,中田秀基 訳『Pythonではじめる機械学習 : scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎』(オライリー・ジャパン, 2017)を大いに参照しました。
6.自分で書いたオリジナルの手書き数字で実験
前回同様自分で書いたオリジナルの手書き数字で実験してみます。
import os
from skimage import io, color
from skimage.transform import resize
import numpy as np
import matplotlib.pyplot as plt
#オリジナルデータを格納するリストの作成
X_original = []
y_original = []
#ディレクトリから画像の読み込み
image_files = os.listdir('./original_images/')
for filename in image_files:
image = io.imread('./original_images/' + filename)
inverted_image = np.invert(image)
gray_image = color.rgb2gray(inverted_image)
resized_image = resize(gray_image, (8, 8))
scaled_image = resized_image * 16
X_original.append(scaled_image)
y_original.append(int(filename[0]))
#画像データを機械学習に適した形にする
X_original_data = np.array(X_original).reshape(10, -1)
y_original_target = np.array(y_original)
#以前に作成したモデルでオリジナルデータの予測
y_original_model = grid_search.predict(X_original_data)
#描画領域の確保
fig, axes = plt.subplots(1, 10, figsize=(15, 15), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.5, wspace=0.5))
#オリジナルデータを「予測値→真の値」というラベルとともに表示
for i, ax in enumerate(axes.flat):
ax.imshow(X_original_data[i].reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest')
label = str(y_original_model[i]) + '→' + str(y_original_target[i])
title_color = "black" if y_original_model[i] == y_original_target[i] else "red"
ax.set_title(label, color=title_color)前回「model.predict(X_original_data)」と書いたところを「grid_search.predict(X_original_data)」に変更しただけです。
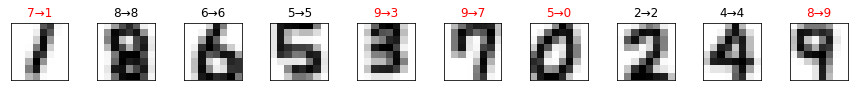
前回よりも結果が悪くなってしまいました。
MNISTデータにより適合しすぎた(オリジナルの手書き数字をターゲットだと考えるなら訓練データに過学習した)せいかもしれません。