scikit-learnでMNIST手書き数字の分類機械学習 – 浅野直樹の学習日記、scikit-learnでMNIST手書き数字の分類機械学習(2) – 浅野直樹の学習日記の続きです。
今回は、しきい値の調節、ニューラルネットワーク、アンサンブルに取り組みます。
1.しきい値の調節
機械学習の目的によっては、単純に正解率のスコアを上げるのではなく、正解率は下がってもよいからできるだけ漏れなく検出してほしいという場合があります。そのような場合にはしきい値を調節します。
0〜9までの10種類の数字を分類するのはややこしいので、8か8以外の数字かを分類するという二項分類の例で考えます。
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.metrics import accuracy_score
from sklearn.metrics import plot_confusion_matrix
import matplotlib.pyplot as plt
#データの読み込み
digits = datasets.load_digits()
#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, shuffle=False)
#8か8以外の数字かでnumpy配列のマスク処理
y_train_8 = (y_train == 8)
y_test_8 = (y_test == 8)
#機械学習モデルの作成
model = svm.SVC()
#作成したモデルで学習
model.fit(X_train, y_train_8)
#学習結果のテスト
y_test_pred = model.predict(X_test)
print('accuracy_score:', accuracy_score(y_test_8, y_test_pred))
#混同行列
plot_confusion_matrix(model, X_test, y_test_8)
plt.show()いつもの要領で学習をして、結果を表示させます。
0.9755555555555555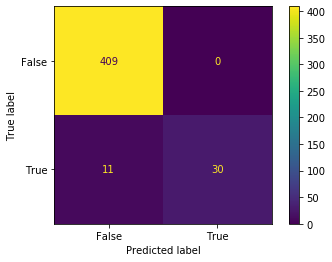
正解率のスコアが0.975…とはなかなかいいですね。
次に、訓練データの混同行列と適合率(precision)・再現率(recall)・F1値を確認してみましょう。
import matplotlib.pyplot as plt
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import precision_score, recall_score
from sklearn.metrics import classification_report
#混同行列
plot_confusion_matrix(model, X_train, y_train_8)
plt.show()
#適合率(precision)・再現率(recall)・F1値の手計算
y_train_pred = model.predict(X_train)
precision_score = precision_score(y_train_8, y_train_pred)
recall_score = recall_score(y_train_8, y_train_pred)
f1_score = (2 * precision_score * recall_score) / (precision_score + recall_score)
print('precision_score:', precision_score)
print('recall_score:', recall_score)
print('f1_score:', f1_score, '\n\n')
#適合率(precision)・再現率(recall)・F1値の一括計算
print(classification_report(y_train_8, y_train_pred))以下の図と文字列が表示されます。
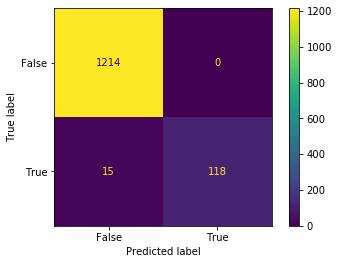
precision_score: 1.0
recall_score: 0.8872180451127819
f1_score: 0.9402390438247012
precision recall f1-score support
False 0.99 1.00 0.99 1214
True 1.00 0.89 0.94 133
accuracy 0.99 1347
macro avg 0.99 0.94 0.97 1347
weighted avg 0.99 0.99 0.99 1347適合率は1.0と完璧ですが、再現率は0.88程度とやや低く、本当は8なのに見逃しているものが15個とけっこうたくさんあります。
適合率が下がることは覚悟で再現率を上げてみましょう。
その前に、適合率と再現率の関係をグラフ化します。
from sklearn.metrics import plot_precision_recall_curve
#適合率―再現率曲線
plot_precision_recall_curve(model, X_train, y_train_8)
plt.show()これだけで簡単きれいに表示されます。
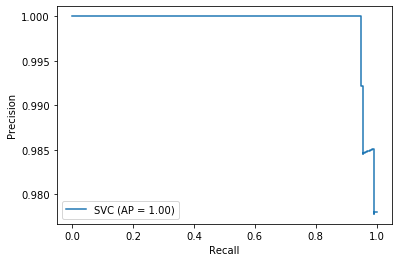
ROC曲線も見てみましょう。
from sklearn.metrics import plot_roc_curve
#ROC曲線
plot_roc_curve(model, X_train, y_train_8)
plt.show()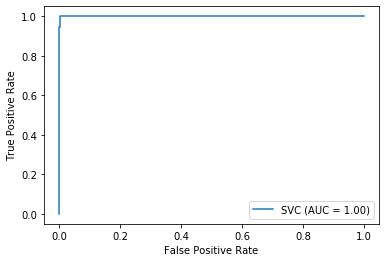
再現率(recall)0.99を狙ってみます。訓練データの中にある133個の8のうち、先ほどは15個を見逃していましたが、見逃してもよいのは1個だけということです。
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
import numpy as np
#訓練データの中で実際には8なのに8ではないと予測したデータ(false_negative)だけをリスト内包表記で抽出
false_negative = [X_train[i] for i in range(len(X_train)) if (y_train_pred[i] == False and y_train_8[i] == True)]
#false_negativeに決定関数を適用した値を取得後、ソートして表示
false_negative_value = model.decision_function(false_negative)
sorted_false_negative_value = np.sort(false_negative_value)
print(sorted_false_negative_value, '\n\n')
#決定関数のしきい値をsorted_false_negative_valueの2番目に小さい数に設定
y_train_pred_lower_threshold = (model.decision_function(X_train) >= sorted_false_negative_value[1])
#新しく設定したしきい値での適合率(precision)・再現率(recall)・F1値の一括計算
print(classification_report(y_train_8, y_train_pred_lower_threshold))
#新しく設定したしきい値での混同行列
disp = ConfusionMatrixDisplay(confusion_matrix(y_train_8, y_train_pred_lower_threshold))
disp.plot()
plt.show()
#新しく設定したしきい値での学習結果のテスト
y_test_pred_lower_threshold = (model.decision_function(X_test) >= sorted_false_negative_value[1])
accuracy_score(y_test_8, y_test_pred_lower_threshold)
#新しく設定したしきい値で学習したテストデータの混同行列
disp = ConfusionMatrixDisplay(confusion_matrix(y_test_8, y_test_pred_lower_threshold))
disp.plot()
plt.show()結果は以下です。
[-0.56471249 -0.5230137 -0.4710125 -0.47010167 -0.46740437 -0.35965516
-0.34701922 -0.21615345 -0.192735 -0.11733131 -0.10970646 -0.06225593
-0.04509709 -0.03724317 -0.02381575]
precision recall f1-score support
False 1.00 1.00 1.00 1214
True 0.99 0.99 0.99 133
accuracy 1.00 1347
macro avg 0.99 1.00 0.99 1347
weighted avg 1.00 1.00 1.00 1347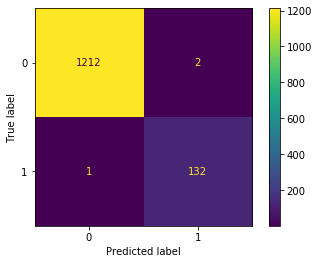
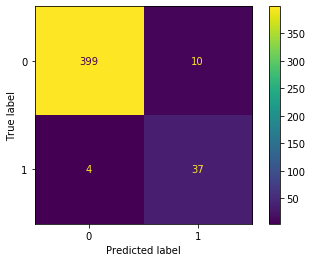
プログラム内のコメントに書いたとおり、false_negative(偽陰性)だけを取り出し、その決定関数の値を参考にして、しきい値を-0.523…に設定しています。
当然ながら、目論見通りに再現率(recall)0.99を達成しています。
テストデータでの結果はそこまでよくありませんが、それでも当初の結果と比べると、見逃しは11個から4個に減少しています。
plot_confusion_matrixはXとyを引数に取るため、しきい値を変更した場合の混同行列はconfusion_matrixとConfusionMatrixDisplayを併用する形で表現しています。
やりたいことはできました。
Aurélien Géron 著,下田倫大 監訳,長尾高弘 訳『scikit-learnとTensorFlowによる実践機械学習』(オライリー・ジャパン, 2018)の3章を主に参照しました。
2.ニューラルネットワーク
scikit-learnでお手軽にニューラルネットワークを試してみます。
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import plot_confusion_matrix
import matplotlib.pyplot as plt
#データの読み込み
digits = datasets.load_digits()
#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, shuffle=False)
#機械学習モデルの作成
model = MLPClassifier(verbose=True, random_state=0)
#学習
model.fit(X_train, y_train)
#学習結果のテスト
y_pred = model.predict(X_test)
print('accuracy_score:', accuracy_score(y_test, y_pred))
#混同行列
plot_confusion_matrix(model, X_test, y_test)
plt.show()いつもの手順でモデルにMLPClassifierを指定しただけです。ニューラルネットワークの雰囲気を醸し出すためにverbose=Trueにしています。よって以下のように出力されます。
Iteration 1, loss = 11.97505127
Iteration 2, loss = 5.72047413
Iteration 3, loss = 3.28455794
(中略)
Iteration 133, loss = 0.00351769
Iteration 134, loss = 0.00345282
Iteration 135, loss = 0.00341083
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
accuracy_score: 0.9244444444444444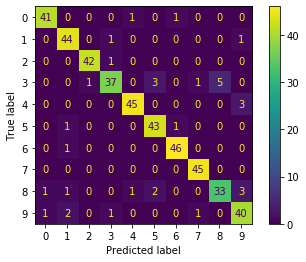
サンプル数が少ないためか、それほどよくない結果ですね。
3.アンサンブル
アンサンブルも試してみます。
#データ関係
from sklearn import datasets
from sklearn.model_selection import train_test_split
#学習モデル関係
from sklearn.ensemble import VotingClassifier
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegressionCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.neural_network import MLPClassifier
#結果の表示
from sklearn.metrics import accuracy_score
from sklearn.metrics import plot_confusion_matrix
import matplotlib.pyplot as plt
#データの読み込み
digits = datasets.load_digits()
#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, shuffle=False)
#スケーリング
X_train = X_train / 16
X_test = X_test / 16
#機械学習モデルの作成
svc = SVC(probability=True)
kn = KNeighborsClassifier()
lr = LogisticRegressionCV(max_iter=500)
rf = RandomForestClassifier()
mlp = MLPClassifier(max_iter=500)
#アンサンブルモデルの作成
hard_voting = VotingClassifier(
estimators=[('svc', svc), ('kn', kn), ('lr', lr), ('rf', rf), ('mlp', mlp)],
voting='hard')
soft_voting = VotingClassifier(
estimators=[('svc', svc), ('kn', kn), ('lr', lr), ('rf', rf), ('mlp', mlp)],
voting='soft')
#学習
hard_voting.fit(X_train, y_train)
soft_voting.fit(X_train, y_train)
#学習結果のテスト
y_hard_pred = hard_voting.predict(X_test)
y_soft_pred = soft_voting.predict(X_test)
print('hard_voting accuracy_score:', accuracy_score(y_test, y_hard_pred))
print('soft_voting accuracy_score:', accuracy_score(y_test, y_soft_pred))
#混同行列
plot_confusion_matrix(hard_voting, X_test, y_test)
plt.show()
plot_confusion_matrix(soft_voting, X_test, y_test)
plt.show()
#個別のモデル
estimators = [svc, kn, lr, rf, mlp]
for estimator in estimators:
estimator.fit(X_train, y_train)
y_individual_pred = estimator.predict(X_test)
print(estimator.__class__.__name__, 'accuracy_score:', accuracy_score(y_test, y_individual_pred))soft_votingのためにSVC(probability=True)としています。また、警告表示を見て、LogisticRegressionCVとMLPClassifierにはmax_iter=500と設定しました。
結果は以下です。
hard_voting accuracy_score: 0.9488888888888889
soft_voting accuracy_score: 0.9444444444444444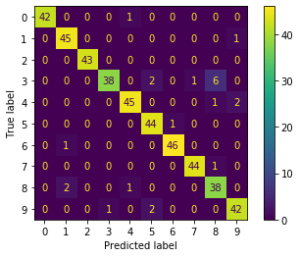
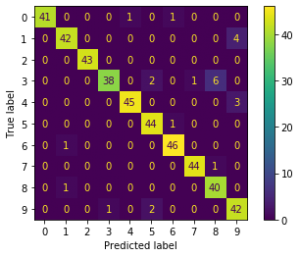
SVC accuracy_score: 0.9488888888888889
KNeighborsClassifier accuracy_score: 0.9644444444444444
LogisticRegressionCV accuracy_score: 0.9288888888888889
RandomForestClassifier accuracy_score: 0.9333333333333333
MLPClassifier accuracy_score: 0.9244444444444444アンサンブルにしたからといって劇的にスコアがよくなるというわけではなさそうです。