浅野直樹の学習日記

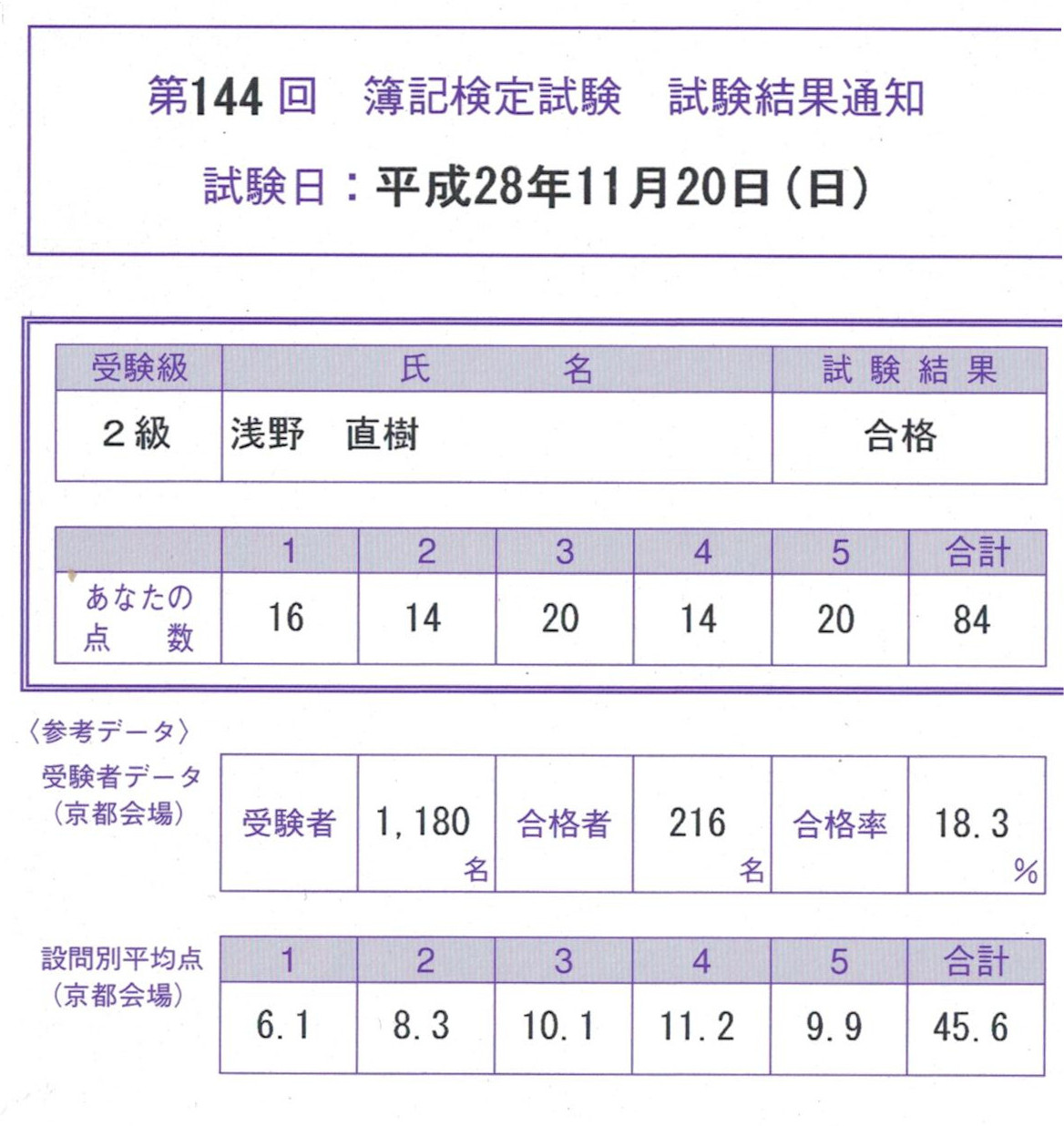
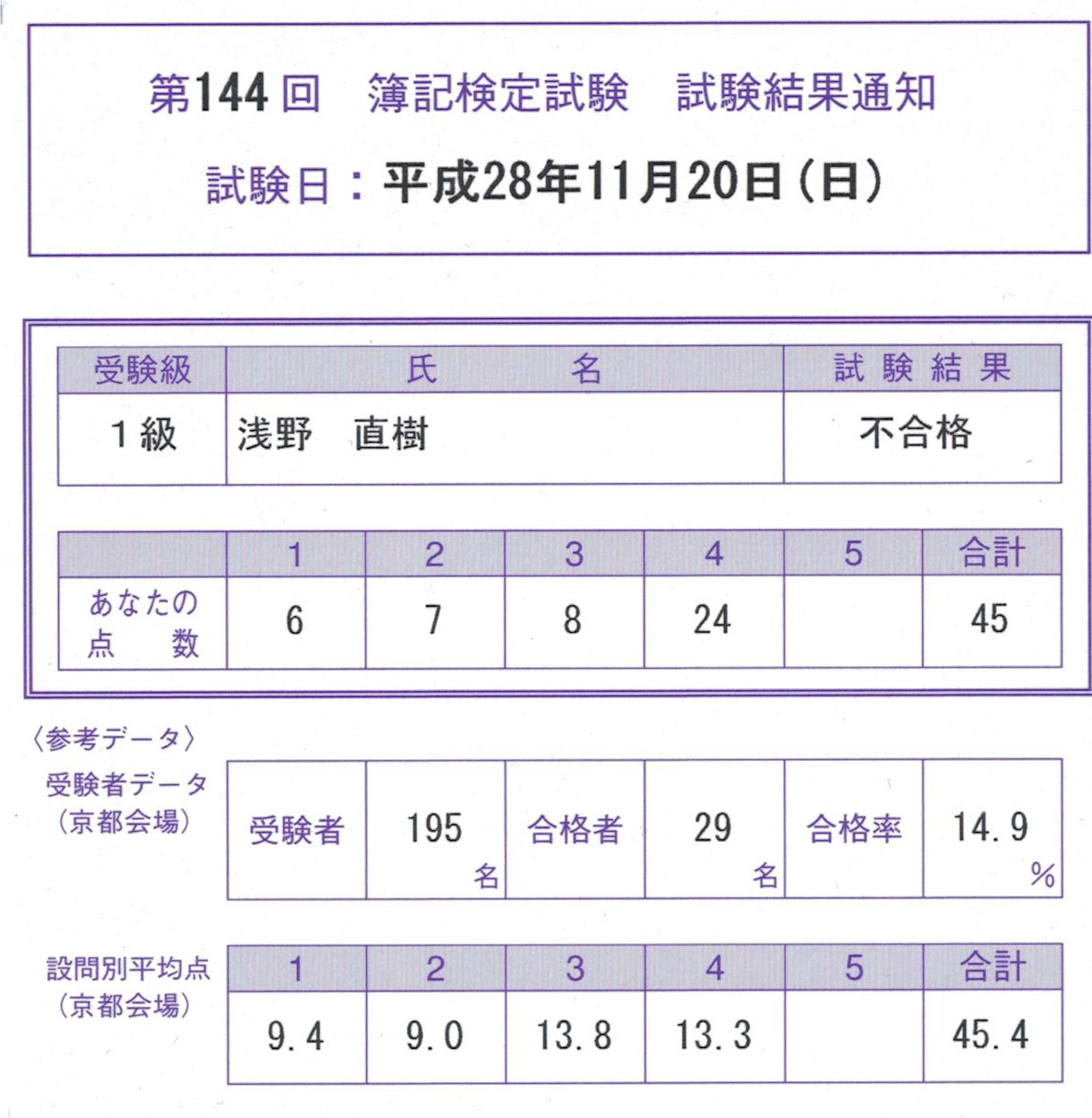
問題

　次の文章を読んで，後記の〔設問１〕及び〔設問２〕に答えなさい。

【事例】
　Ａは，平成２３年１１月１０日，Ｂに対し，弁済期を平成２４年１１月１０日として，１０００万円を貸し付けた（以下，この貸付けに基づく貸金債権を「甲債権」という。）。しかし，Ｂは，弁済期にこれを返済しなかった。
　そこで，ＡがＢの現在の財産状況を調査したところ，Ｂの営む店舗の経営状態が悪化し，甲債権のほかにも，多額の借入金や取引先に対する買掛金の合計１億円余りが弁済期を過ぎても未払となっていること，Ｂの所有する不動産にはその評価額以上に抵当権が設定されており，平成２５年１月３１日を弁済期とする５００万円の売掛金債権（以下「乙債権」という。）をＣに対して有するほか，Ｂには見るべき資産がないことが判明した。
　そこで，平成２５年２月２５日，Ａは，Ｂに代位して，乙債権の支払を求める訴えをＣに対して提起した（以下，この訴えに係る訴訟を「訴訟１」という。）。

〔設問１〕（(1)と(2)は，独立した問題である。）
(1) Ｂは，平成２５年３月１４日，訴訟１に係る訴状の送達を受けたＣから問い合わせを受けて，訴訟１が第一審に係属中であることを知った。Ｂは，甲債権については，平成２４年１２月１０日にＡから免除を受けたとしてその存在を争うとともに，乙債権については，自己に支払うようＣに求めたいと考えている。
　ア この場合，Ｂは，訴訟１において，民事訴訟法上，どのような手段を採ることができるか，理由を付して述べなさい。
　イ 裁判所は，審理の結果，甲債権は存在せず，乙債権は存在すると判断した場合，どのような判決をすべきか，Ａが提起した訴訟１に係る訴え及びアでＢが採った手段のそれぞれについて説明しなさい。

(2) Ｂが訴訟１の係属の事実を知らないうちに，訴訟１について，甲債権は存在すると認められるが，乙債権が存在するとは認められないとして，請求棄却判決がされ，この第一審判決が確定した。その後，Ｂが，Ｃに対し，乙債権の支払を求めて訴えを提起した（以下，この訴えに係る訴訟を「訴訟２」という。）ところ，訴訟２の過程において，訴訟１についての上記確定判決の存在が明らかになった。この場合において，訴訟２の受訴裁判所はどのような判決をすべきか，当該受訴裁判所が，審理の結果，訴訟１の口頭弁論終結時において甲債権が存在していたと判断したときと，これが存在していなかったと判断したときとに分けて説明しなさい。

【事例（続き）】（〔設問１〕の問題文中に記載した事実は考慮しない。）
　Ｄは，Ｂに対して，平成２５年２月１０日を弁済期とする１５００万円の売掛金債権を有しているが，同年４月半ば，Ｄの取引先でＣとも取引関係があるＥから，ＡのＣに対する訴訟１が第一審に係属中であると知らされた。
　そこで，Ｄは，顧問弁護士と相談した結果，Ａが甲債権を有することを争う必要はないが，このままではＡが乙債権の弁済による利益を独占し，自らが弁済を受ける機会を失ってしまうこととなるので，それを避けたいと考えるに至った。

〔設問２〕
この場合，Ｄは，訴訟１において，民事訴訟法上，どのような手段を採ることができるか，理由を付して述べなさい。

練習答案

以下民事訴訟法についてはその条数のみを示す。

［設問１］
（１）
　ア
　　この場合、Bは、訴訟１において、民事訴訟法４７条１項の独立当事者参加という手段を採ることができる。
　　訴訟の結果によって権利が害されることを主張する第三者又は訴訟の目的の全部若しくは一部が自己の権利であることを主張する第三者は、その訴訟の当事者の双方又は一方を相手方として、当事者としてその訴訟に参加することができる（４７条１項）。
　　甲債権の存在が認められ、乙債権の存在が認められずに、請求棄却判決が訴訟１でされると、乙債権の不存在についての既判力（１１４条１項）がBにも及ぶ。当事者が他人のために原告又は被告となった場合のその他人には既判力が及ぶ（１１５条１項２号）ところ、Aのような代位債権者（民法４２３条１項）は、１１５条１項２号の当事者であるからである。そうなるとBは乙債権を行使できなくなるのでその権利が害されるため、独立当事者参加ができる。
　　甲債権と乙債権の双方の存在が認められて、請求認容判決が訴訟１でされると、甲債権というBにとっての債務が認められる結果乙債権を行使できなくなるので、やはり権利が害される。
　　甲債権の存在が認められないと乙債権にかかわらず却下判決が訴訟１でされることになるが、その場合は乙債権という訴訟の目的が自己の権利であるとBは主張できるので、独立当事者参加をすることができる。
　　以上より、Bは、Aを相手方として甲債権の不存在の確認を、Cを相手方として乙債権の自己への支払いをそれぞれ求めて、独立当事者参加をすることができる。
　イ
　　裁判所は、審理の結果、甲債権は存在せず、乙債権は存在すると判断した場合、Aが提起した訴訟１に係る訴えについては却下判決を、BのAを相手方とする請求については請求認容判決を、BのCを相手方とする請求については請求認容判決をすべきである。
　　後二者についてはBの請求がそのまま認められているので特に説明する必要もない。前者については、甲債権の存在が認められれば代位債権者としてAは当事者となる（２８条）が、認められなければ当事者とならず、訴えが不適法でその不備を補正することができなくなり、訴えを却下することになる（１４０条）。

（２）
　　問題文の場合において、訴訟２の受訴裁判所は、審理の結果、訴訟１の口頭弁論終結時において甲債権が存在していたと判断したときと、これが存在していなかったと判断したときのいずれも、請求棄却判決をすべきである。
　　（１）で述べたように、この場合に乙債権の不存在についての既判力がBに及ぶので、請求棄却判決となる。訴訟２の受訴裁判所が甲債権についてどのように判断しようとも、訴訟１では甲債権が認められ、乙債権について審理が尽くされた上でそれが存在しないという結論に至り、Cもその結論を信頼しているので、いずれの場合も請求棄却判決をすべきである。

［設問２］
　この場合、Dは、訴訟１において、民事訴訟法４７条１項の独立当事者参加という手段を採ることができる。Dは、Bに債権者代位して、訴訟１の目的である乙債権の行使が自己の権利であると主張することができるからである。

以上

修正答案

以下民事訴訟法についてはその条数のみを示す。

［設問１］
（１）
　ア
　　この場合、Bは、訴訟１において、民事訴訟法４７条１項の独立当事者参加という手段を採ることができる。
　　Bとしては、Cに対して乙債権の支払いを求める別訴を提起することがまず考えられる。しかし、AがBに代位してCに対して乙債権の支払いを求める訴訟１をすでに提起してこれが係属しているので、二重起訴に該当するため、この別訴を提起することはできない（１４２条）。
　　次に、BがAの側に補助参加（４２条）することが考えられるが、これが認められA側が勝訴したとしても乙債権はAに支払われてしまいBとして支払いを受けることができないので、無意味である。
　　そこで最後に独立当事者参加（４７条）を検討する。Bにとっては、Aの訴訟遂行がまずくて乙債権の存在が裁判所によって認定されなかったとしたら自己に権利が害されることになると言えるし、訴訟１で訴訟の目的となっている乙債権がAが代位できる債権ではなく自己の権利であると主張することができるとも言える。いずれにせよ４７条１項の要件を満たす。
　　この場合、Bは、Aに対しては甲債権の不存在確認の、Cに対しては乙債権の支払いの請求をそれぞれ立てることになる。甲債権が不存在であればそもそもAによる訴訟１が不適法であり、そのことを争っているのだから、これは二重起訴には該当しない。これが二重起訴に当たるとすると、いったん債権者代位訴訟が係属すると、債務者として被保全債権の存在を争うことができなくなり、不合理である。
　　独立当事者参加をするためには、統一的な審判という観点から、請求の非両立性も要請される。甲債権が存在すればBではなくAが当事者となり乙債権はAに支払うべきであり、逆に甲債権が存在しなければAではなくBが当事者となり乙債権はBに支払うべきであり、請求の非両立性という条件も満たす。

　イ
　　裁判所は、審理の結果、甲債権は存在せず、乙債権は存在すると判断した場合、Aが提起した訴訟１に係る訴えについては却下判決を、BのAを相手方とする請求については請求認容判決を、BのCを相手方とする請求については請求認容判決をすべきである。
　　後二者についてはBの請求がそのまま認められているので特に説明する必要もない。前者については、甲債権の存在が認められれば代位債権者としてAは当事者となるが、認められなければ当事者とならず、訴えが不適法でその不備を補正することができなくなり、訴えを却下することになる（１４０条）。

（２）
　　問題文の場合において、訴訟２の受訴裁判所は、審理の結果、訴訟１の口頭弁論終結時において甲債権が存在していたと判断したときは請求棄却判決を、存在していなかったと判断したときは乙債権の存在の有無に応じて請求認容判決または請求棄却判決をすべきである。
　　訴訟１で乙債権に関してAが当事者となっている。これは訴訟担当である。そうすると１１５条１項２号により、被担当者であるBにも既判力が及ぶ。このような場合に既判力が及ばないとすると、CにとってはAとの訴訟で一度請求棄却判決を得てもBとの訴訟に再び応じなければならなくなり、酷であると同時に不経済である。
　　ただし、甲債権が存在しなかった場合にまで既判力がBに及ぶとすると、Bにとって酷であり不合理である。甲債権が存在しなければそもそも訴訟１が不適法だからである。Bとしては（１）で述べたように独立当事者参加ができるとしても、訴訟１の係属を知らなければどうしようもない。他方でCとしてはBに対して訴訟告知をすることで二重応訴の負担を免れることができると言える。

［設問２］
　［設問１］で述べたように、甲債権が存在するとすると、訴訟１の既判力はBに及ぶ。そうなると結果的に訴訟１の効力がDにも及ぶことになる。Bに既判力が及ぶということは、そのBの債権者であるDが代位することもできなくなるからである。そこで、Dとしては、訴訟１で何らかの手段を採る必要に迫られる。
　［設問１］（１）アで述べたのと同じ理由で、別訴の提起は二重起訴に抵触し、補助参加は無意味であり、独立当事者参加をすることができる。Dは債権者としてBに代位しようとしているのだから、基本的にBと同じように考えればよい。共同訴訟参加（５２条）については、訴訟１が先に係属している以上、甲債権が存在すればAのみが当事者となり、甲債権が非存在でAが当事者ではなくなって初めてDが当事者となる可能性が出てくるので、共同訴訟人とはならないため不可である。
以上

感想

練習ではかなりひどい答案を作ってしまいました。［設問２］は結論・記述方法ともこれでよいのか不安です。

問題

　次の文章を読んで，後記の〔設問１〕から〔設問３〕までに答えなさい。

１．Ｘ株式会社（以下「Ｘ社」という。）は，日本国内において不動産の開発及び販売等を行う監査役会設置会社であり，金融商品取引所にその発行する株式を上場している。

２．Ｙ株式会社（以下「Ｙ社」という。）は，日本国内において新築マンションの企画及び販売等を行う取締役会設置会社であり，監査役を置いている。Ｙ社が発行する株式は普通株式のみであり，その譲渡による取得にはＹ社の承認を要するものとされている。
　Ｙ社の発行済株式のうち，７５％はＸ社及びその子会社（以下，Ｘ社を含め「Ｘグループ」という。）が，１５％はＹ社の取締役であるＡが，１０％は関東地方を中心に住居用の中古不動産の販売等を行うＺ株式会社（以下「Ｚ社」という。）がそれぞれ保有している。なお，Ｚ社の発行済株式の６７％はＡが保有し，同社の取締役はＡ及びＡの親族のみである。

３．Ｘ社は，平成２３年９月，Ｙ社の行う事業をＸグループ内の他社に統合する方向で検討を始め，その後，Ａに対し，Ａ及びＺ社が保有するＹ社株式をＸ社に売却するよう求めた。しかし，Ａは，Ｙ社との資本関係が失われることによって生じ得るＺ社の事業展開への不安を訴えて回答を留保し，その後のＸ社による説得にも応じなかった。

４．Ｘ社は，平成２４年６月１日，取締役会を開催し，同年９月１日をもってＹ社をＸ社の完全子会社とする旨の株式交換契約（以下「本件株式交換契約」という。）を締結することを適法に決定した。また，Ｙ社でも，同年６月１日，取締役会を開催し，本件株式交換契約を締結することを適法に決定した。
　これらの決定を受けて，Ｘ社とＹ社との間で本件株式交換契約が正式に締結された。本件株式交換契約においては，Ｙ社株主に対しＹ社株式１０株につきＸ社株式１株を交付する，すなわち，Ｘ社とＹ社との間の株式交換比率（以下「本件交換比率」という。）を１対０．１とする旨が定められた。

５．Ｘ社では，同月２９日，定時株主総会が開催され，本件株式交換契約の承認に関する議案が適法に可決された。

６．Ｙ社でも，同日，定時株主総会（以下「本件総会」という。）が適法な招集手続に基づき開催された。本件総会には，本件株式交換契約の承認に関する議案及びＡの取締役からの解任に関する議案が提出された。
　Ａは，本件総会の議場において，株主としての地位に基づき，議長である代表取締役Ｂに対し，自らが取締役から解任される理由について質問をした。これに対してＢは，「それはあなたもわかっているはずであり，答える必要はない。」と回答し，質疑を打ち切った。Ａ及びＺ社は，本件総会に提出された上記各議案に反対したが，いずれもＸグループ各社の賛成により可決された。

７．Ａは，同年７月，本件交換比率の妥当性について独自に検討し，算定を行うこととした。その結果，同年８月，Ａとしては，Ｙ社株主に対しＹ社株式１０株につきＸ社株式３株を交付するのが妥当であるとの結論に至った。

〔設問１〕
　Ａは，Ａを取締役から解任する旨の本件総会の決議の効力を争うことができるか。

〔設問２〕
　Ａは，Ｙ社に対し，本件交換比率の妥当性を検討するためであることを明らかにして，本件交換比率をＹ社が算定するために使用したＹ社の一切の会計帳簿及びこれに関する資料の閲覧を請求した。Ｙ社は，この請求を拒むことができるか。なお，Ｙ社の会計帳簿及びこれに関する資料は書面をもって作成されているものとする。

〔設問３〕
　本件交換比率を不当と考えるＡが，
　① 本件株式交換契約に基づく株式交換の効力発生前に会社法上採ることができる手段
　② 本件株式交換契約に基づく株式交換の効力発生後に会社法上採ることができる手段として，それぞれどのようなものが考えられるか。

練習答案

以下会社法についてはその条数のみを示す。

［設問１］
　取締役は、いつでも、株主総会の決議によって解任することができる（３３９条１項）。XグループはY社の発行済株式のうち７５％を保有していたので、定足数及び議決数は満たしている（３４１条）。
　取締役は、株主総会において株主から特定の事項について説明を求められた場合には、当該事項について必要な説明をしなければならない（３１４条本文）。Bは取締役であり、Aは株主である。A自らが取締役から解任される理由についての質問は特定の事項について説明を求めることであり、株主総会の目的である事項に関しないものではないし、その説明をすることにより株主の共同の利害を著しく害する場合その他正当な理由がある場合でもない。よって３１４条但書には該当せず、Bは必要な説明をしなければならない。「それはあなたもわかっているはずであり、答える必要はない。」との回答は、とうてい説明になっていない。以上より、本件株主総会には３１４条違反がある。
　株主総会の決議が法令に違反する場合には、株主は、株主総会の決議の日から３か月以内に、訴えをもって当該決議の取消しを請求することができる（８３１条１項前段、同１号）。先に見たように本件株主総会の決議の方法が法令に違反しているので、株主であるAは、平成２４年９月２９日までに、訴えをもって、Aを取締役から解任する旨の本件総会の決議の取消しを請求して、その効力を争うことができる。

［設問２］
　発行済株式の１００分の３以上の数の株式を有する株主は、株式会社の営業時間内は、いつでも、会計帳簿又はこれに関する資料の閲覧の請求をすることができる（４３３条１項１号）。その請求があったときは、株式会社は、４３３条２項各号に該当する場合を除き、これを拒むことができない（４３３条２項柱書）。
　AはY社の発行済株式の１５％を保有しているので、１００分の３以上の数の株式を有する株主である。よって本問のY社の会計帳簿及びこれに関する資料の閲覧をY社の営業時間内はいつでもすることができる。
　本件交換比率如何で割り当てられるX社株式数が変動するので、それはY社株主Aの権利の行使に関する調査である（４３３条２項１号及び２号には該当しない）。この閲覧によって知り得た事実を利益を得て第三者に通報するためではないし、過去にそのような通報をしたことも認められない（４３３条２項４号及び５号には該当しない）。Aは、関東地方を中心に住宅用の中古不動産の販売等を行うZ社の発行済株式の６７％を保有し同社の取締役でもあるので、日本国内において新築マンションの企画及び販売等を行うY社と実質的に競争関係にある事業を営んでいると言えるので、４３３条２項３号に該当するように見える。しかし同号はそれにより株主の共同の利益が害されることを防ぐ趣旨であり、同号に該当するからといって一律に閲覧請求を拒めるとすると株主としての正当な権利行使が妨げられてしまうので、株主の共同の利益が害される危険性と権利行使の正当性を考慮して閲覧請求を拒めるかどうかを決するべきである。本件では特に株主の共同の利害が害されることを窺わせる事情がない一方で、権利行使の正当性ははっきり認められるので、Y社はAによる閲覧請求を拒むことはできない。

［設問３］
　①
　　本件株式交換契約に基づく株式交換の効力発生前に会社法上採ることができる手段として、株主による取締役の行為の差止め（３６０条１項）及び本件株式交換契約を承認したY社株主総会の決議の取消しの訴え（８３１条１項）が考えられる。
　②
本件株式交換契約に基づく株式交換の効力発生後に会社法上採ることができる手段として、株式会社の株式交換無効の訴え（８２８条１項１１号）が考えられる。

以上

修正答案

以下会社法についてはその条数のみを示す。

［設問１］
　取締役は、いつでも、株主総会の決議によって解任することができる（３３９条１項）。XグループはY社の発行済株式のうち７５％を保有していたので、定足数及び議決数は満たしている（３４１条）。
　取締役は、株主総会において株主から特定の事項について説明を求められた場合には、当該事項について必要な説明をしなければならない（３１４条本文）。Bは取締役であり、Aは株主である。A自らが取締役から解任される理由についての質問は特定の事項について説明を求めることであり、株主総会の目的である事項に関しないものではないし、その説明をすることにより株主の共同の利害を著しく害する場合その他正当な理由がある場合でもない。よって３１４条但書には該当せず、Bは必要な説明をしなければならない。「それはあなたもわかっているはずであり、答える必要はない。」との回答は、とうてい説明になっていない。以上より、本件株主総会には３１４条違反がある。
　株主総会の決議が法令に違反する場合には、株主は、株主総会の決議の日から３か月以内に、訴えをもって当該決議の取消しを請求することができる（８３１条１項前段、同１号）。先に見たように本件株主総会の決議の方法が法令に違反しているので、株主であるAは、平成２４年９月２９日までに、訴えをもって、Aを取締役から解任する旨の本件総会の決議の取消しを請求して、その効力を争うことができる。説明義務をおよそ果たさいないということは重大な違反なので、裁量棄却（８３１条２項）の余地はない。

［設問２］
　発行済株式の１００分の３以上の数の株式を有する株主は、株式会社の営業時間内は、いつでも、会計帳簿又はこれに関する資料の閲覧の請求をすることができる（４３３条１項１号）。その請求があったときは、株式会社は、４３３条２項各号に該当する場合を除き、これを拒むことができない（４３３条２項柱書）。
　AはY社の発行済株式の１５％を保有しているので、１００分の３以上の数の株式を有する株主である。よって本問のY社の会計帳簿及びこれに関する資料の閲覧をY社の営業時間内はいつでもすることができる。
　本件交換比率如何で割り当てられるX社株式数が変動するので、それはY社株主Aの権利の行使に関する調査である（４３３条２項１号及び２号には該当しない）。この閲覧によって知り得た事実を利益を得て第三者に通報するためではないし、過去にそのような通報をしたことも認められない（４３３条２項４号及び５号には該当しない）。請求者の側で会社にどのような資料があるのか詳細はわからないため、「本件交換比率をＹ社が算定するために使用したＹ社の一切の会計帳簿及びこれに関する資料」とすることで理由を明らかにしたと言える。
　Aは、関東地方を中心に住宅用の中古不動産の販売等を行うZ社の発行済株式の６７％を保有し同社の取締役でもあるので、日本国内において新築マンションの企画及び販売等を行うY社と実質的に競争関係にある事業を営んでいると言える。よって４３３条２項３号に該当する。同号は１号及び２号とは異なり請求者の主観的意図を要件とはしていないので、その事業を営んでいるという客観的な事情により該当すると判断すべきである。
　以上より、Y社は、４３３条２項３号に該当するとして、この請求を拒むことができる。

［設問３］
　①
　　本件株式交換契約に基づく株式交換の効力発生前に会社法上採ることができる手段として、本件株式交換契約を承認したY社株主総会の決議の取消しの訴え（８３１条１項）が考えられる。「株主総会等の決議について特別の利害関係を有する者が議決権を行使したことによって、著しく不当な決議がされたとき」（８３１条１項３号）に該当する。Xグループは株式交換の相手方であり、株式交換比率という決議について特別の利害関係を有する者である。交換比率を操作することにより、他の株主の犠牲のもとで、正当な価格よりも安くY社を手に入れることができるからである。
　　このように株主総会の決議の取消しが認められるとしても、係争中に株式交換が行われてしまう可能性がある。そこで、会社法では本件のような株式交換の事前差止については規定されていないので【注：平成２６年改正前】、民事保全法の仮処分を用いることが考えられる。
　　他方で、不当な比率での株式交換そのものをやめさせたいのではなく、適正な金銭を得てY社株主という地位を脱退したいということであれば、株式買取請求権を行使することが考えられる（７８５条）。Aは株主総会で本件決議に反対しているので、株主総会に先立って反対する旨を通知していれば（問題文からはこの通知をしていたかどうかは定かではない）、７８５条２項１号イの要件を満たす。
　②
　　本件株式交換契約に基づく株式交換の効力発生後に会社法上採ることができる手段として、株式会社の株式交換無効の訴え（８２８条１項１１号）が考えられる。しかし、交換比率の不当性は、無効とせずとも事後的に損害賠償により調整できるため、無効事由とはならないと解すべきである。上記①で述べた８３１条１項３号の決議についても突き詰めると不当な合併比率という問題に行き着くため、本件では無効とはならない。
　　そこで、事後的な損害賠償として、４２９条による取締役の第三者への責任追及をすることが考えられる。会社株主は会社の所有者であるので４２３条により会社について損害を回復させるのが筋であるという考え方がある。しかし本件のように大株主によって少数株主が搾取されるような場合は、会社全体が損害を被っているというよりも、少数株主が損害を被っていると言える。よってAはY社の株主であるけれども個人的に４２９条１項のY社代表取締役であるBの責任を追及することができる。Bが本件株式交換という職務を行うについて、正当な交換比率で契約を締結するという任務を懈怠し、そのことにつき悪意又は重大な過失があったことが認められる。
以上

感想

［設問２］は判例を読んで結論を変えました。［設問３］は出題趣旨に挙げられていることを全部書こうとするとものすごく大変です。

日商簿記検定３級・２級の受験記録 – 浅野直樹の学習日記の続編で、日商簿記検定２級と１級を受験したときの記録です。先に結果を書いておくと、２級が８４点で合格、１級が４５点で不合格でした。

１．簿記２級の勉強

前回の受験であと１点のところまでいけていましたし、今回は１級を受けるので、２級のための勉強はしませんでした。１級の勉強をしてから２級の問題を解くと簡単に思えました。試験当日も満点を取るつもりで臨んだのですが、いくつかミスをしてしまいました。

簿記は上の級の勉強をすると、その級だけの勉強をしていると見えないことも見えてくるような気がします。

２．簿記１級の勉強

３級、２級とお世話になった「スッキリ」シリーズを使いました。

スッキリわかる日商簿記1級商業簿記・会計学 作　者：　 出版社：　TAC株式会社出版事業部 発売日：　2015年12月01日

１級になると冊数が多くて大変です。

特に商業簿記は覚えるべきことが多くて厳しかったです。会計学も手をつけにくかったです。工業簿記は理解したつもりでしたが試験本番では混乱して結果を出せませんでした。原価計算は数学に近いので原理を理解すればできると思っていました。

３．感想

団体の会計を担当する際にあったほうがよい素養を身につけ、財務諸表を読んだり会計学に近いことを教えたりするための基礎知識を得るという当初の目標はおよそ達成できたと思います。簿記の勉強は着実に進んでいるという手応えを得やすいので精神衛生上もよいですね。その反面で結果がシビアに点数化され、しかもだいたい想像していた点数より悪いという厳しさがあります。