前から気になっていた機械学習に手を出し始めました。 何冊かの本を読み、インターネット上の資料も見て、ようやく少し理解できました。 自分の理解を整理するために、scikit-learnを使ったMNIST手書き数字の分類という典型的な例を示してみます。
Recognizing hand-written digits — scikit-learn 0.24.2 documentationの焼き直しです。In-Depth: Decision Trees and Random Forests | Python Data Science Handbookも参考にしています。
jupyter notebook上で順次実行するという形で試していますが、他の環境でも本質的な部分には変わりはないと思います。
1.データの読み込みと確認
まずはデータを読み込んで確認します。
import matplotlib.pyplot as plt
from sklearn import datasets
####MNIST手書き数字のデータ読み込みと確認####
digits = datasets.load_digits()
print(digits.keys())
####読み込んだ手書き数字データの画像表示####
#描画領域の確保
fig, axes = plt.subplots(10, 10, figsize=(15, 15), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.5, wspace=0.5))
#確保した描画領域に読み込んだ画像の最初の100枚を表示
for i, ax in enumerate(axes.flat):
ax.imshow(digits.images[i], cmap=plt.cm.gray_r, interpolation='nearest')
ax.set_title(digits.target[i])これを実行すると次のような文字と画像が表示されます。
dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR'])
digitsという変数名で読み込んだデータのimagesというプロパティに画像のデータが、targetというプロパティに正解ラベル(その人が何の数字を書いたか)が入っています。
2.データの前処理
機械学習に適した形になるようデータを前処理します。具体的に言うと、サンプル数×特徴量数の2次元配列を作るということです。
まず、先ほど画像として表示したdigits.imagesの形式を確認してみましょう。
#imagesプロパティの形状を取得して表示
image_shape = digits.images.shape
print(image_shape)
#サンプル数の取得
n_samples = len(digits.images)
print(n_samples)
#念のために上記二種類のやり方で取得したサンプル数が一致することを確認
print(image_shape[0] == n_samples)次のように表示されます。
(1797, 8, 8)
1797
Trueサンプル数が1797というのはいいとして、特徴量の部分が8×8の2次元の配列になっており、全体で3次元の配列になってしまっています。
画像として表示するためには2次元の配列であるほうが都合がよいのですが、機械学習のためには1次元のほうがよいです。
そこで次のように変形します。
my_data = digits.images.reshape((n_samples, -1))
print(my_data.shape)reshapeメソッドにマイナス1を渡すと適当にうまく値を定めてくれます。ここでは「my_data = digits.images.reshape((n_samples, 64))」と同じことになります。
(1797, 64)これでデータの前処理は完了です。
今回は画像に適した2次元配列の特徴量から機械学習に適した1次元配列の特徴量へと手作業で変換しましたが、実はdigitsデータには最初から1次元配列に変換されたデータが含まれています。digits.dataです。
import numpy as np
flag = np.allclose(my_data, digits.data)
print(flag)同じデータになっていることが確認されました。
True
3.訓練データとテストデータに分け、機械学習のモデルを作成し、学習させる
いよいよ機械学習の本体的な部分です。
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.metrics import accuracy_score
#訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(my_data, digits.target, shuffle=False)
#機械学習モデルの作成
model = svm.SVC()
#作成したモデルで学習
model.fit(X_train, y_train)
#学習結果のテスト
y_model = model.predict(X_test)
accuracy_score(y_test, y_model)たったのこれだけです。難しいことは背後でscikit-learnがやってくれます。
0.94888888888888891に近いほどいい値であり、0.95くらいならまずまずではないでしょうか。
せっかくなので、もう一つ別のモデルでも試してみましょう。
from sklearn.ensemble import RandomForestClassifier
#別のモデルの作成
another_model = RandomForestClassifier()
#別のモデルで学習
another_model.fit(X_train, y_train)
#別のモデルの学習結果のテスト
y_another_model = another_model.predict(X_test)
accuracy_score(y_test, y_another_model)結果の数字は先ほどより少し悪くなりました。
0.9333333333333333モデルやパラメータの選択が機械学習の腕の見せ所になるのですが、ここではこれ以上深入りしません。
4.結果の可視化
どの数字をどの数字に間違えたのかを混同行列で示してみましょう。
from sklearn.metrics import plot_confusion_matrix
plot_confusion_matrix(model, X_test, y_test)
plt.show()きれいなヒートマップが表示されます。
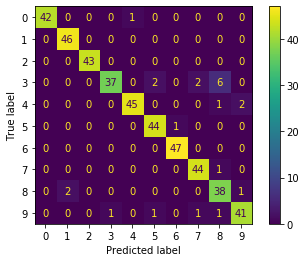
本当は3なのに8だと予測してしまったものが6つあるということがわかります。
今度は予測値と真の値を画像で表示してみましょう。
先ほどとは逆に1次元配列の特徴量を2次元配列の特徴量へと復元します。「X_test[i].reshape(8, 8)」の部分です。
#描画領域の確保
fig, axes = plt.subplots(10, 10, figsize=(15, 15), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.5, wspace=0.5))
#テストデータの最初の100枚を「予測値→真の値」というラベルとともに表示
for i, ax in enumerate(axes.flat):
ax.imshow(X_test[i].reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest')
label = str(y_model[i]) + '→' + str(y_test[i])
title_color = "black" if y_model[i] == y_test[i] else "red"
ax.set_title(label, color=title_color)このような画像が表示されます。

上から2行目、左から5列目のデータで、正しくは5であるところを6と予測してしまっています。画像を目で見るとこれは仕方ないかなという気もします。
せっかくなので予測を間違えたものだけを取り出して見てみましょう。
データの画像を表示する部分は基本的に先ほどと同じですが、描画領域の100に対してデータが23しかなくて list index out of rangeエラーが表示されるのを防ぐため、「if i+1 >= len(failed_test): break」を最後に加えています。
#テストデータのサンプル数を取得
n_test = len(X_test)
#予測を間違えたテストデータだけを予測値と真の値とともにリスト内包表記で抽出
failed_test = [{'data':X_test[i], 'y_model':y_model[i], 'y_test':y_test[i]} for i in range(n_test) if y_model[i] != y_test[i]]
#描画領域の確保
fig, axes = plt.subplots(10, 10, figsize=(15, 15), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.5, wspace=0.5))
#予測を間違えたテストデータを「予測値→真の値」というラベルとともに表示
for i, ax in enumerate(axes.flat):
ax.imshow(failed_test[i]['data'].reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest')
label = str(failed_test[i]['y_model']) + '→' + str(failed_test[i]['y_test'])
ax.set_title(label, color='red')
if i+1 >= len(failed_test): break次のような画像が表示されます。

予測を間違えるのも頷ける判別しづらい画像が並んでいます。
5.自分で書いたオリジナルの手書き数字で実験
ここからはオマケです。しかし一番苦労した部分でもあります。
自分で書いたオリジナルの手書き数字を判別できるか実験してみました。
MNISTデータと同じような画像にして同じようなデータにするのが大変でした。
試行錯誤の過程は省いて結論だけ言います。
GIMPを使い、32px×32pxの背景を1600%に拡大して表示して、5px×5pxの鉛筆を選んでマウスで数字を書きました。
プログラムを実行しているファイルが存在している階層にoriginal_imagesディレクトリを作成し、そこに0.png, 1.png, …, 9.pngという名前で画像を保存しました。
画像を読み込んで変形し、先ほど学習したモデルで予測をするコードは以下です。
import os
from skimage import io, color
from skimage.transform import resize
#オリジナルデータを格納するリストの作成
X_original = []
y_original = []
#ディレクトリから画像の読み込み
image_files = os.listdir('./original_images/')
for filename in image_files:
image = io.imread('./original_images/' + filename)
inverted_image = np.invert(image)
gray_image = color.rgb2gray(inverted_image)
resized_image = resize(gray_image, (8, 8))
scaled_image = resized_image * 16
X_original.append(scaled_image)
y_original.append(int(filename[0]))
#画像データを機械学習に適した形にする
X_original_data = np.array(X_original).reshape(10, -1)
y_original_target = np.array(y_original)
#以前に作成したモデルでオリジナルデータの予測
y_original_model = model.predict(X_original_data)
#描画領域の確保
fig, axes = plt.subplots(1, 10, figsize=(15, 15), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.5, wspace=0.5))
#オリジナルデータを「予測値→真の値」というラベルとともに表示
for i, ax in enumerate(axes.flat):
ax.imshow(X_original_data[i].reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest')
label = str(y_original_model[i]) + '→' + str(y_original_target[i])
title_color = "black" if y_original_model[i] == y_original_target[i] else "red"
ax.set_title(label, color=title_color)なぜか色が反転していたのでnp.invert関数でその補正をして、rgb画像からgray画像に変換し、32×32の画像を8×8にリサイズしています。
MNISTデータは0〜16で色の濃さを表現していることに気づかずハマリました。scikit-imageで何も指定せずにファイルを読み込むと0〜1で色の濃さが表現されているので、それを単純に16倍しました。
結果の表示は以下の通りです。
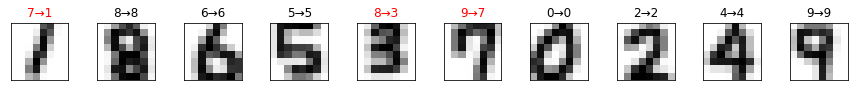
まずまずではないでしょうか。