浅野直樹の学習日記

平行線と線分の比

平行線と線分の比とは、右の図でBC // DEのとき、次の２つの事柄が成り立つことです。

 

 

（ア）の証明はそれほど難しくありません。

 

【証明】

△ABCと△ADEにおいて

BC // DEより平行線の同位角は等しいので

∠ABC＝∠ADE…①

∠ACB＝∠AED…②

①、②より２つの角がそれぞれ等しいので

△ABC∽△ADE

対応する辺の比は等しいので

AB:AD＝AC:AE＝BC:DE

 

これで（ア）は証明できました。問題は（イ）です。直感的には成り立ちそうですが、きちんと証明するとなると意外に苦労します。

 

平行線と線分の比の証明その１

補助線を引いて平行四辺形を作るやり方です。中学数学の教科書に載っているのはおそらくこれです。

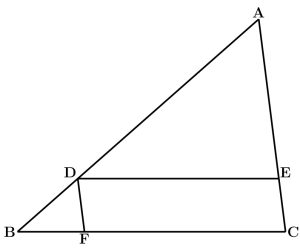
【証明】

Dを通りACに平行な直線を引き、その直線とBCとの交点をFとする。

△ADEと△DBFにおいて

BC // DEより平行線の同位角は等しいので

∠ADE＝∠DBF…①

AC // DFより平行線の同位角は等しいので

∠DAE＝∠BDF…②

①、②より２つの角がそれぞれ等しいので

△ADE∽△DBF

対応する辺の比は等しいので

AD:DB＝AE:DF…③

四角形DECFは平行四辺形なので

DF＝EC

このことと③より

AD:DB＝AE:EC

 

平行線と線分の比の証明その２

私は補助線を引いて平行四辺形を作ることが思いつかず、相似比から直接考えました。

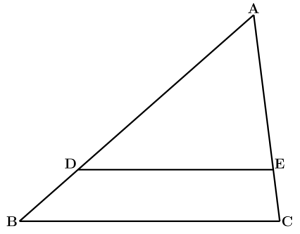
【証明】

（ア）の証明より

△ABC∽△ADEであり、その相似比をa:bとすると

AB:AD＝AC:AE＝a:bとなる。

このことより、ある正の数m, nを用いて（2020/9/28「任意の正の数」を「ある正の数」に訂正）

AB＝am, AD＝bm

AC＝an, AE＝bn

と表すことができる。

DB＝AB−AD＝am−bm＝m(a−b)

EC＝AC−AE＝an−bn＝n(a−b)

となり、

AD:DB

＝bm:m(a-b)

＝b:(a−b)

AE:EC

＝bn:n(a−b)

＝b:(a−b)

となるので、

AD:DB＝AE:ECが成り立つ。

 

比と実際の長さを混同しないように注意する必要がありますが、こうすれば補助線を引くことなしに相似比から直接証明できます。