数学IIIで習う放物線の応用問題としてパラボラアンテナの性質を示すのがおもしろいのでまとめます。
パラボラアンテナの原理と放物線の性質 | 高校数学の美しい物語と放物線の接線の方程式と光線の反射 | 受験の月を参考にさせてもらいました。この両サイトにはいつもお世話になっております。数学がそこまで得意だというわけでもない高校生にも理解できるようにさらにわかりやすく提示するのが私の仕事だと思っています。両サイトの作者に数学力ではとてもかないません。
1.問題
パラボラアンテナの対称軸に対して平行に入射した信号は「焦点に」「同時に」届くことを証明せよ。
これを以下のような小問に分解するとわかりやすいです。
パラボラアンテナの対称軸が$y$軸、頂点が原点になるように設定し、そのパラボラアンテナが表す曲線を$y=ax^2(a>0)$とする。このとき、以下の問いに答えよ。
(1) $y=ax^2$上の点A$(t, at^2)(t\ne{0})$における接線の方程式を求めよ。
(2) 曲線$y=ax^2$の焦点をF、(1)で求めた接線と$y$軸との交点をBとするとき、△FABがFA$=$FBの二等辺三角形であることを示せ。
(3) 点$(t, k)(k>at^2)$をPとし、点Aを通り(1)で求めた接線と直交する直線と$y$軸との交点をCとするとき、∠PAC$=$∠FACであることを示せ。
(4) $t$の値にかかわらずPA$+$AFが一定であることを示せ。
2.図
問題文を図にすると以下のようになります。
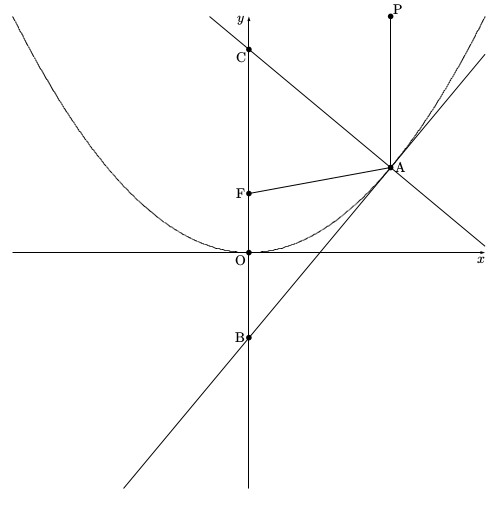
3.小問1
$y’=2ax$よりA$(t, at^2)$での接線の傾きは$2at$となるので、求める直線は
$y-at^2=2at(x-t)$
$y=2atx-at^2$
となる。
(これは微分の定番問題ですね。$y^2=4px$で表される横向きの放物線でも同じように考えることができますが、逆関数の微分が必要となってやや面倒です。多くの高校では逆関数の微分よりも先に放物線などの二次曲線を習いますから。)
4.小問2
この曲線の式を変形すると$x^2=4\cdot\frac1{4a}y$になるので、放物線の定義より、焦点は$(0, \frac1{4a})$である。
(1)で求めた接線の式$y=2atx-at^2$の$x$に$0$を代入すると$y=-at^2$となるので、Bの座標は$(0, -at^2)$である。
よってFB$=\frac1{4a}+at^2$である。
また、FA$=\sqrt{t^2+(at^2-\frac1{4a})^2}=\sqrt{a^2t^4+\frac12t^2+\frac1{16a^2}}=\sqrt{(at^2+\frac1{4a})^2}=at^2+\frac1{4a}$
以上よりFA$=$FBとなるので△FABはFA$=$FBの二等辺三角形である。
(この小問のように△FABが二等辺三角形であることに着目するという発想がなかなか思いつかないので、小問を付して誘導するのがよいと思います。)
5.小問3
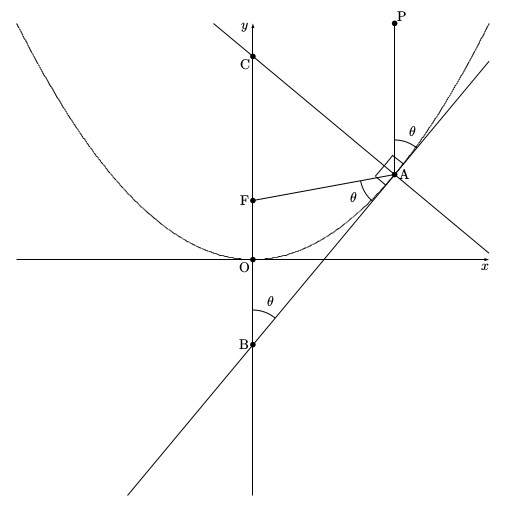
(1)で求めた接線と直線PAとのなす角を$\theta$とする。
PA // FBであり、平行線の同位角は等しいので、∠FBA$=\theta$である。
(2)より△FABはFA$=$FBの二等辺三角形であり底角が等しいので∠FAB$=\theta$である。
図より∠PAC$=90^{\circ}-\theta$、∠FAC$=90^{\circ}-\theta$となるので、∠PAC$=$∠FACである。
(これでPからAへと入射した信号が入射角$=$反射角となるように反射すると焦点Fを通ることが示されました。)
6.小問4
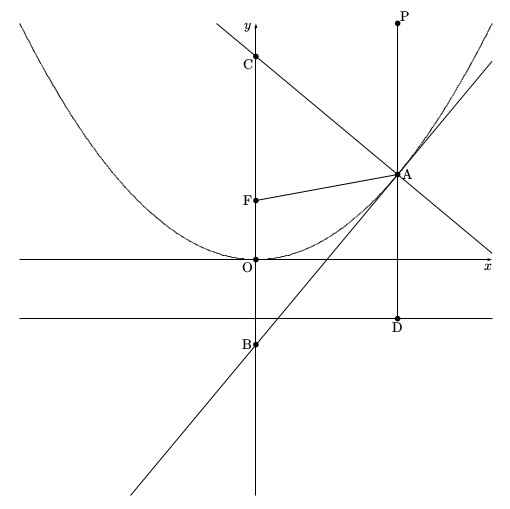
放物線の定義より、この放物線の準線は$y=-\frac1{4a}$である。そして点$(t, -\frac1{4a})$をDとすると、AF$=$ADである。
AD$=at^2+\frac1{4a}$なので、AF$=at^2+\frac1{4a}$である。
以上より
PA$+$AF$=(k-at^2)+(at^2+\frac1{4a})=k+\frac1{4a}$となり、$t$の値にかかわらず一定である。
(これで焦点Fへと至る道のりが等しくなることがわかるので速さの等しい信号がどこから入射しようとも「同時に」届くことが示されました。)
7.おわりに
$t\ne{0}$のときはFABが三角形にならないので別途考える必要がありますが、∠PAC$=$∠FAC$=0^{\circ}$、PA$+$AF$=k+\frac1{4a}$であることは明らかです。角度をtanの加法定理で扱う方法も捨てがたいです。
[…] パラボラアンテナの性質を証明する放物線の応用問題 – 浅野直樹の学習日記 […]