第7章 推測統計(検定)
7.1 検定の考え方
(例題1)
あるサイコロを1000回振ったときに1の目が200回出た。このサイコロが正しく作られているかどうかを統計的に検定せよ。
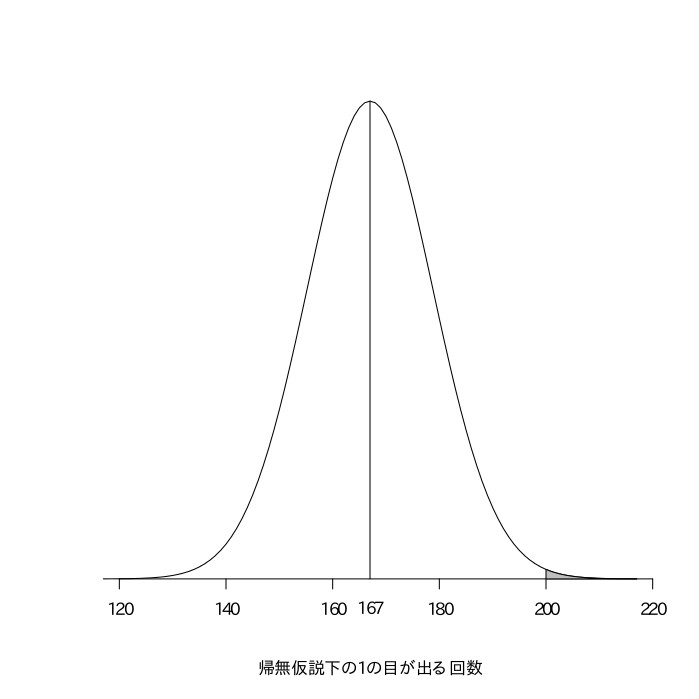
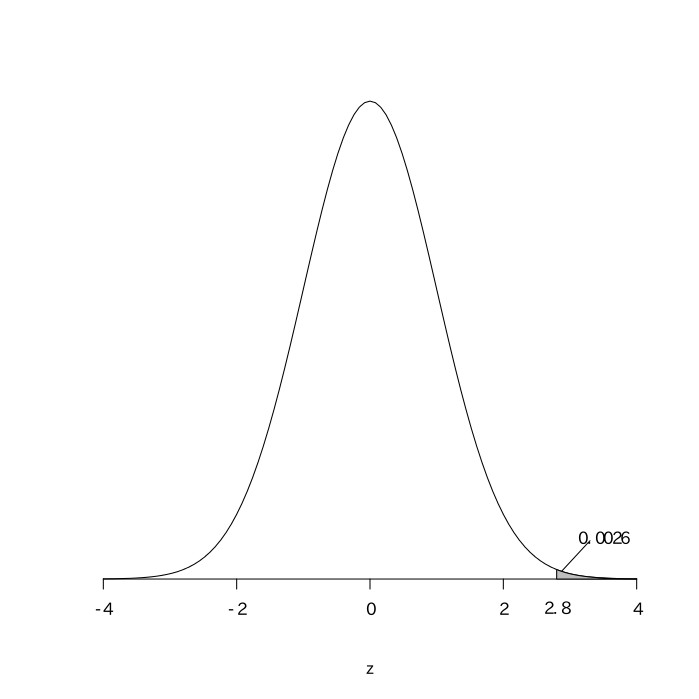
このサイコロが正しく作られていると仮定したときに(帰無仮説)、問題文のような結果になる確率を考え、それが5%以下であれば帰無仮説を棄却して、このサイコロが正しく作られていないということ(対立仮説)を採用する。このサイコロが正しく作られていると仮定すると、そのサイコロを1000回振ったときに1の目が出る回数は二項分布(1000, 0.167)に従い、サイコロを振る回数(n)が十分大きいので、正規分布$(1000\times0.167, 1000\times0.167\times(1-0.167))=(167, 139.1)$で近似できる。実際には1の目が200回出たので、これを標準正規分布上で考えると、$\frac{200-167}{\sqrt{139.1}}=2.80$となり、標準正規分布表から$z=2.80$の部分を読み取ると0.4974であるので、$0.5-0.4974=0.0026 < 0.025$より、帰無仮説を棄却できる。
以上より、統計的に、このサイコロが正しく作られていない(いかさまサイコロである)と言える。
↓
【問題1】
あるサイコロを100回振ったときに1の目が20回出た。このサイコロが正しく作られているかどうかを統計的に検定せよ。
(例題2)
長嶋茂雄の生涯打率は8094打数2471安打の.305、王貞治の生涯打率は9250打数2786安打の.301であった。このことから、長嶋のほうが王よりも打率が高いと言えるかどうかを統計的に検定せよ。
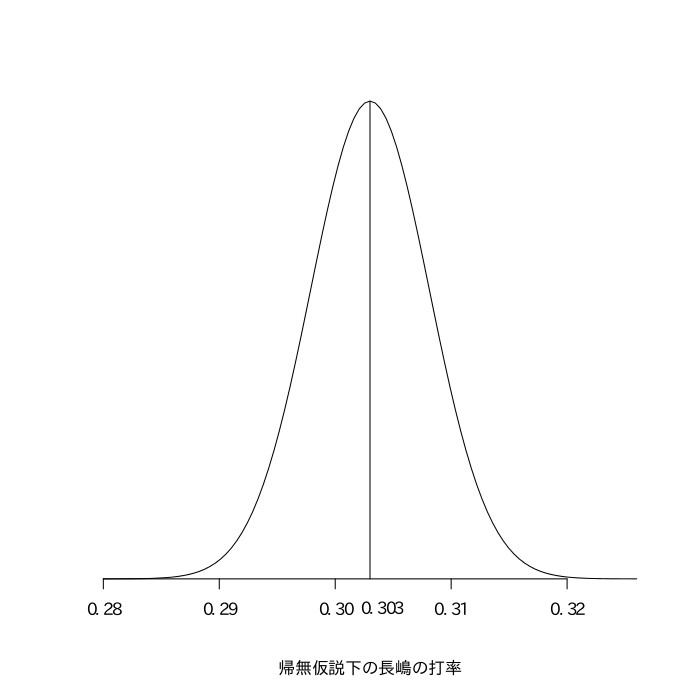
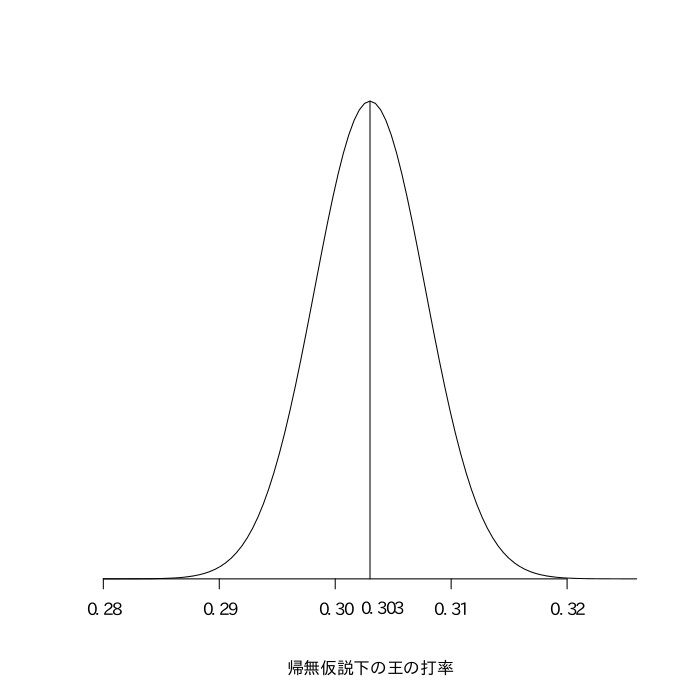
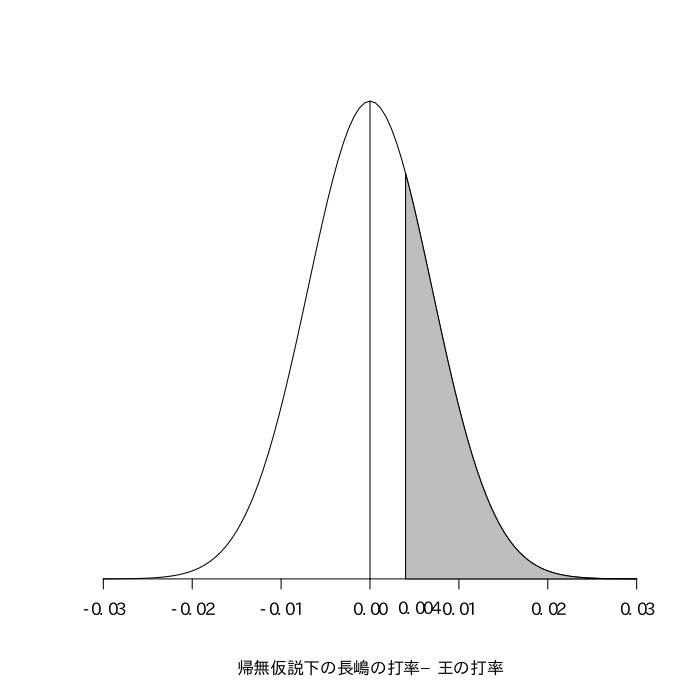
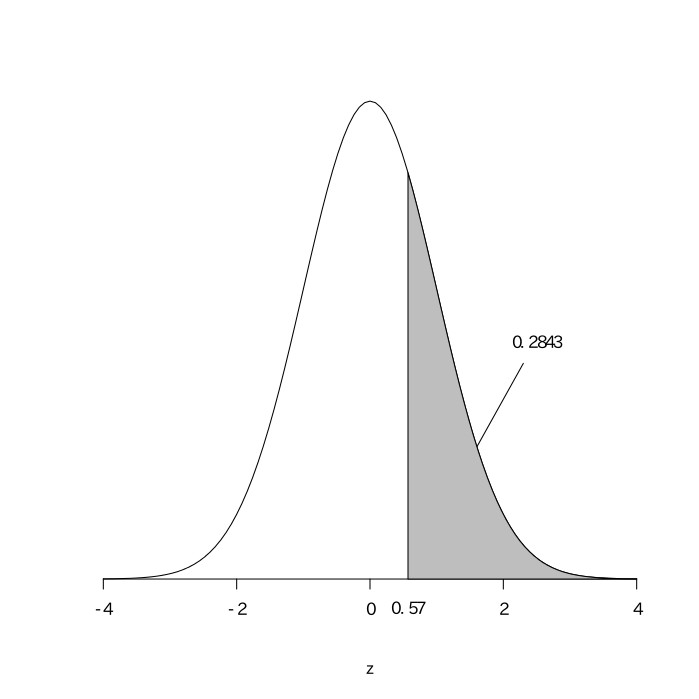
長嶋と王の打率が等しいと仮定したときに(帰無仮説)、問題文のような結果になる確率を考え、それが5%以下であれば帰無仮説を棄却して、長嶋のほうが王よりも打率が高いということ(対立仮説)を採用する。長嶋と王の両方を合わせた打率は17344打数5257安打の.303である。.303で8094打数のとき安打数は二項分布(8094, 0.303)に従い、打数(n)が十分大きいので、$(8094\times0.303, 8079\times0.303\times0.697)=(2452.5, 1709.4)=(2452.5, 41.345^2)$の正規分布で近似できる。これを打数8094で割って、打率は$(0.303, 0.0051081^2)=(0.303, 0.00002609)$の正規分布で近似できる(帰無仮説のもとでの長嶋の打率)。同様に、.303で9250打数のときの打率は、$(0.303, 0.00002283)$の正規分布で近似できる(帰無仮説のもとでの王の打率)。正規分布の加法性より、(帰無仮説のもとでの長嶋の打率)$-$(帰無仮説のもとでの王の打率)は、$(0303-0.303, 0.00002609+0.00002283)=(0, 0.00004892)$の正規分布となる(正規分布をなす2つの集団からの要素を引き算して新しい集団を作る場合に、新しい集団の平均は2つの集団の平均を引いたものになるが、分散は2つの集団の分散を足したものになる)。(実際の長嶋の打率)$-$(実際の王の打率)$=0.004$であるので、これを先ほどの正規分布を標準化したものの上で考えると、$\frac{0.004}{\sqrt{0.00004892}}=\frac{0.004}{0.006994}=0.57$となり、標準正規分布表から$z=0.57$の部分を読み取ると0.2157であるので、$0.5-0.2157=0.2843>0.05$より帰無仮説を棄却できない。
以上より、統計的に、長嶋のほうが王よりも打率が高いと言うことはできない。
$-$(マイナス)
$=$(イコール)
↓
【問題2】
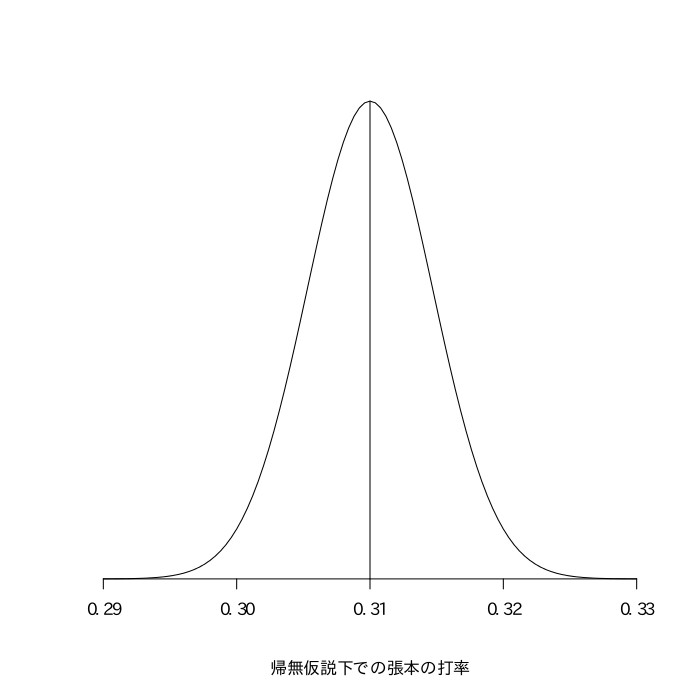
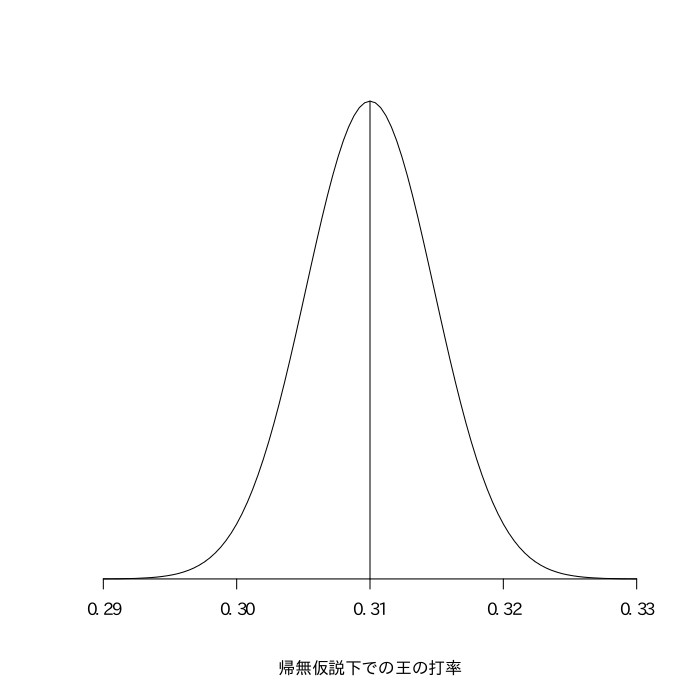
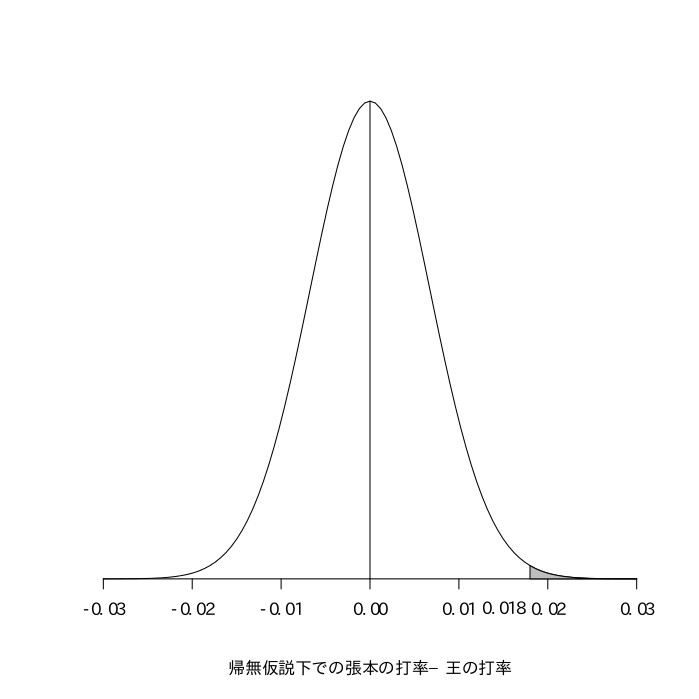
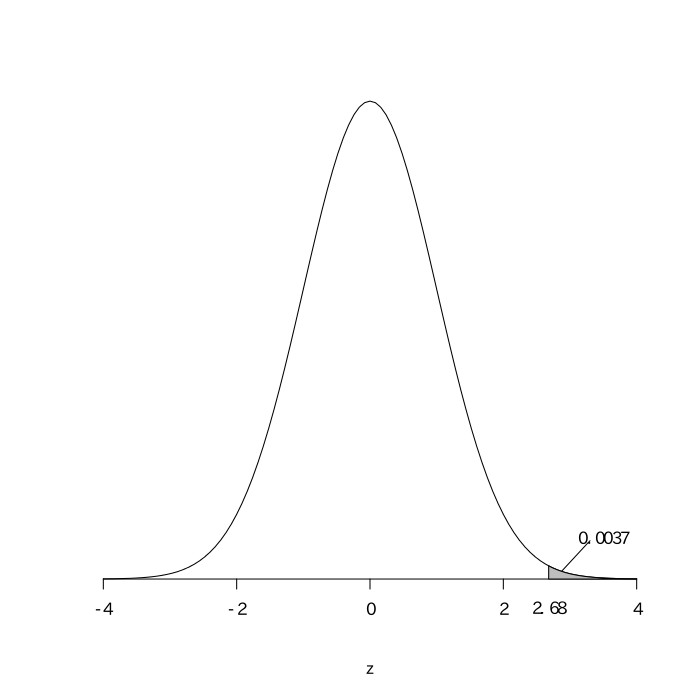
張本勲の生涯打率は9666打数3085安打の.319、王貞治の生涯打率は9250打数2786安打の.301であった。このことから、張本のほうが王よりも打率が高いと言えるかどうかを統計的に検定せよ。
7.2 z検定(大標本)
(例題3)
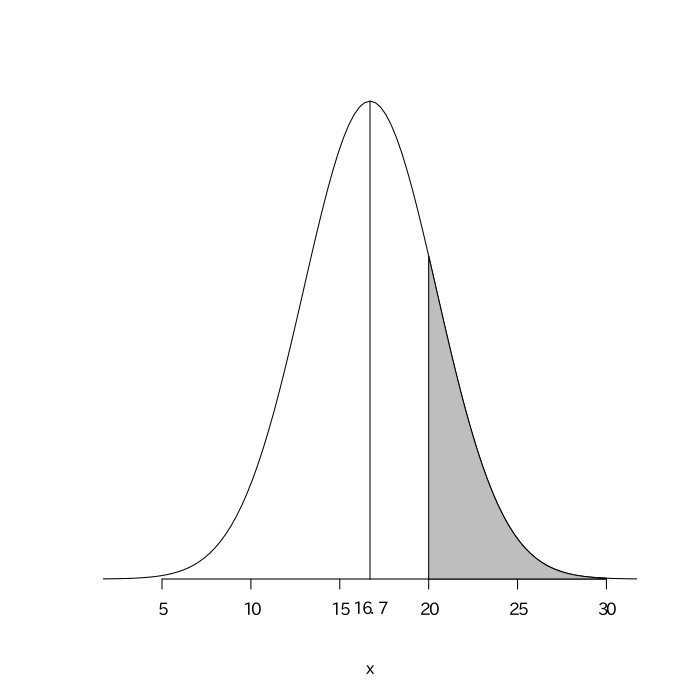
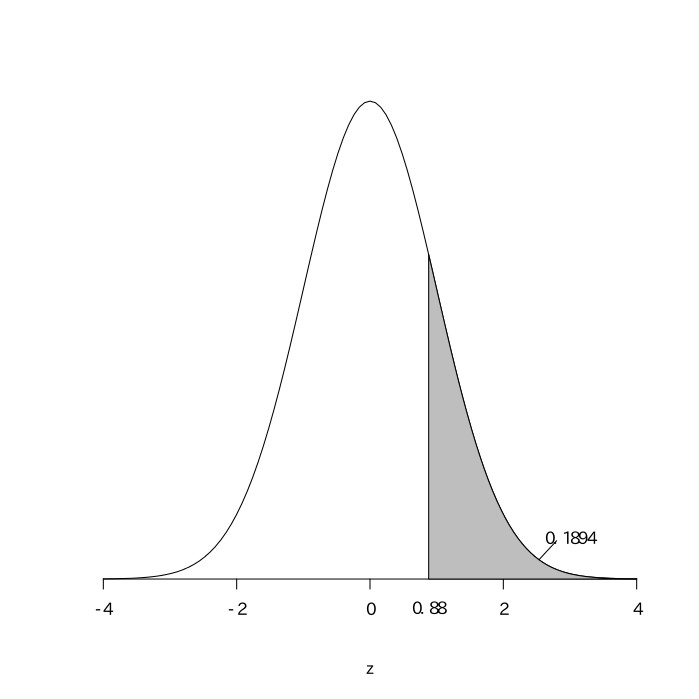
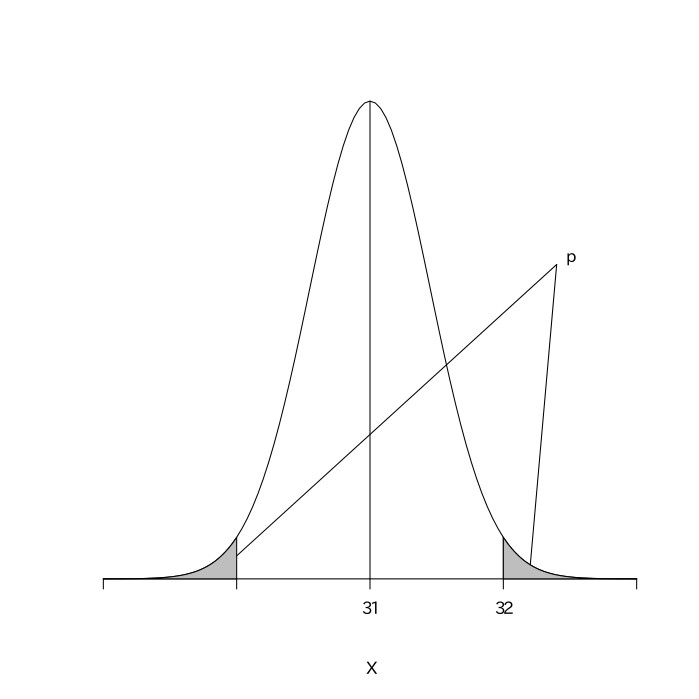
ある工業製品の平均重量は31.0gであることがわかっている。その工業製品を製造する機械が故障したので、新しい機械に取り替えた。新しい機械で作られたその工業製品から50個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたと言えるかどうか、統計的に検定せよ。
機械を新しくする前と後とでこの工業製品の平均重量は異ならないと仮定する(帰無仮説)。${母集団平均}=31.0$である。標本数が多いので、${母集団分散}={標本分散}=10.24$と考える。標本平均の集合をXとすると、Xは平均が$31.0$、分散が$10.24\div50=0.2048$の正規分布に従い、$\frac{X-31.0}{\sqrt{0.2048}}$は平均が0、分散が1の標準正規分布になる。今、新しい機械で作られたこの工業製品から50個を無作為抽出したものの平均重量が32.0だったので、これをXに代入して計算すると$\frac{32.0-31.0}{\sqrt{0.2048}}$
$=\frac{1}{0.4525}$
$=2.21$
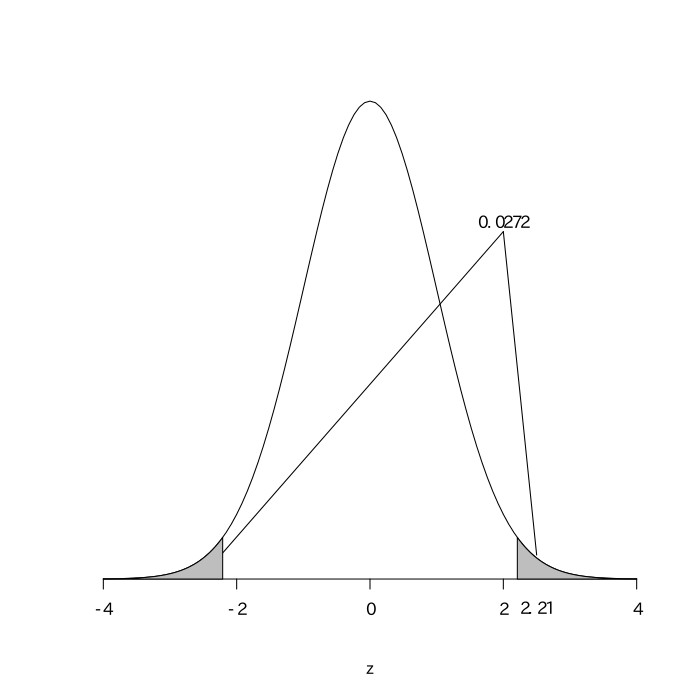
となる。$z=2.21$を標準正規分布表で読むと$0.4864$であり、$p=(0.5-0.4864)\times2=0.0272( < 0.05)$なので、帰無仮説を棄却できる。
以上より、統計的に、機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたと言える。
↓
【問題3】
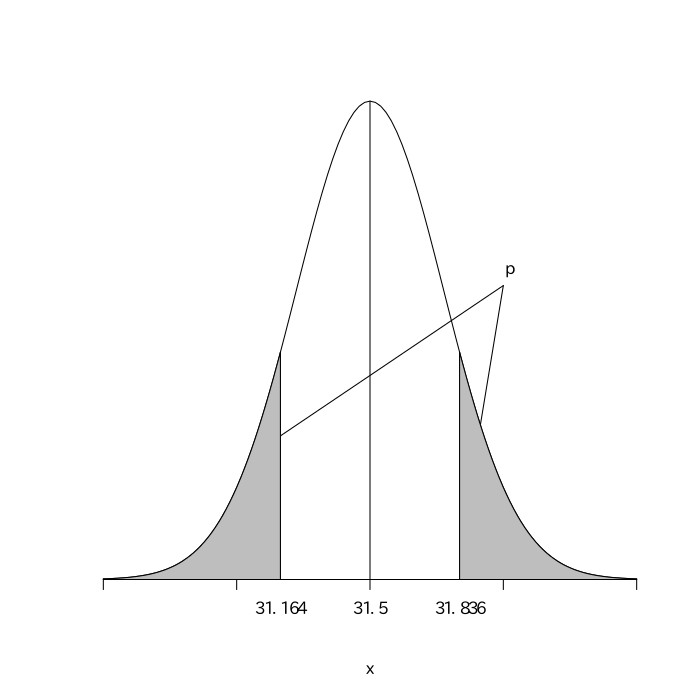
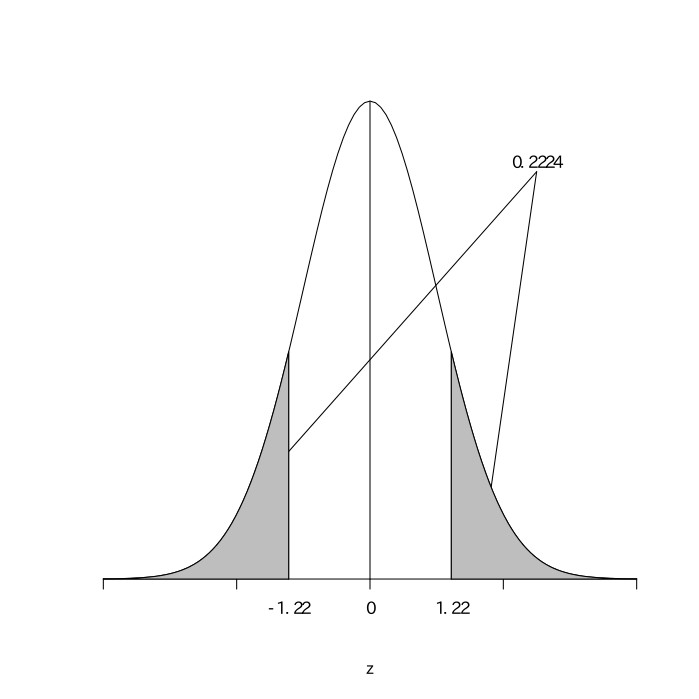
ある怪しい男が両替屋に金貨を100枚持ってきた。その重さを測定すると、以下の通りであった。この金貨が本物の金貨かどうかを統計的に検定せよ。なお、本物の金貨の平均重量は31.5gである。
| 29.92 | 27.73 | 31.34 | 31.67 | 37.04 | 33.86 | 30.08 | 31.94 | 24.20 | 30.08 |
| 28.37 | 32.75 | 29.18 | 29.39 | 35.59 | 32.79 | 27.92 | 36.20 | 32.81 | 30.69 |
| 32.27 | 30.24 | 33.63 | 33.20 | 26.58 | 34.38 | 27.72 | 31.43 | 29.88 | 25.33 |
| 30.94 | 31.36 | 28.56 | 28.94 | 28.63 | 29.18 | 26.54 | 30.85 | 35.31 | 31.19 |
| 31.86 | 28.29 | 31.18 | 31.92 | 27.79 | 34.33 | 34.88 | 34.53 | 29.26 | 28.24 |
| 31.00 | 28.43 | 35.75 | 34.73 | 32.99 | 29.29 | 31.93 | 30.76 | 34.89 | 33.63 |
| 29.85 | 30.78 | 30.49 | 34.20 | 27.25 | 32.34 | 29.09 | 29.36 | 31.78 | 31.45 |
| 29.95 | 32.59 | 33.23 | 27.99 | 32.67 | 35.32 | 31.37 | 31.11 | 26.80 | 24.9 |
| 32.20 | 29.80 | 30.85 | 36.41 | 36.68 | 28.61 | 33.25 | 28.78 | 33.75 | 37.31 |
| 29.65 | 31.45 | 29.29 | 34.15 | 30.87 | 30.88 | 32.53 | 31.29 | 32.90 | 27.81 |
(例題4)
ある工業製品を製造する機械が故障したので、新しい機械に取り替えた。古い機械で作られたその工業製品から40個を無作為抽出して重量を調査したとき、その標本の平均重量は31.0g、その標本の標準偏差は2.8gであった。新しい機械で作られたその工業製品から50個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたと言えるかどうか、統計的に検定せよ。
機械を新しくする前と後とでこの工業製品の平均重量は異ならないと仮定する(帰無仮説)。その平均重量を$\mu$とおく。標本サイズが大きいので、${母集団分散}={標本分散}$と考える。機械を新しくする前の標本平均の集合を$X_1$とすると、$X_1$は平均が$\mu$、分散が$7.84\div40=0.196$の正規分布に従う。
機械を新しくした後の標本平均の集合を$X_2$とすると、$X_2$は平均が$\mu$、分散が$10.24\div50=0.2048$の正規分布に従う。
これらの差$X_1-X_2$は、正規分布の加法性より、平均が0、分散が$0.196+0.2948=0.4008$の正規分布に従う。これを$\sqrt{0.4008}$で割った$\frac{X_1-X_2}{\sqrt{0.4008}}=\frac{X_1-X_2}{0.6331}$は平均が0、標準偏差が1の標準正規分布となる。
ここに$X_1=31.0, X_2=32.0$を代入すると
$\frac{-1}{0.6331}$
$=-1.58$
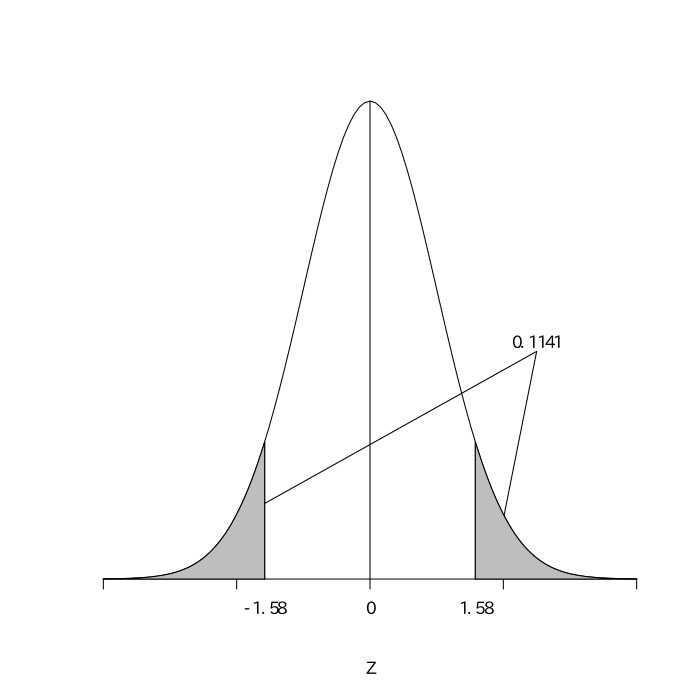
となる。$z=1.58$を標準正規分布表で読むと$0.4429$であり、$p=(0.5-0.4429)\times2=0.1141( > 0.05)$なので、帰無仮説を棄却できない。
以上より、統計的に、機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたとは言えない。
【問題4】
ある血圧を下げる薬の効果を確かめるために、A群(40人)にはこの薬を投与し、B群(50人)には偽薬を投与して血圧を測定した結果、A群の血圧の平均は110で標準偏差は15、B群の血圧の平均は125で標準偏差は20だった。この薬に血圧を下げる効果があるかどうかを、統計的に検定せよ。
7.3 t検定(小標本)
(例題5)
ある工業製品の平均重量は31.0gであることがわかっている。その工業製品を製造する機械が故障したので、新しい機械に取り替えた。新しい機械で作られたその工業製品から10個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたと言えるかどうか、統計的に検定せよ。ただし、この工業製品の重量は正規分布しているとする。
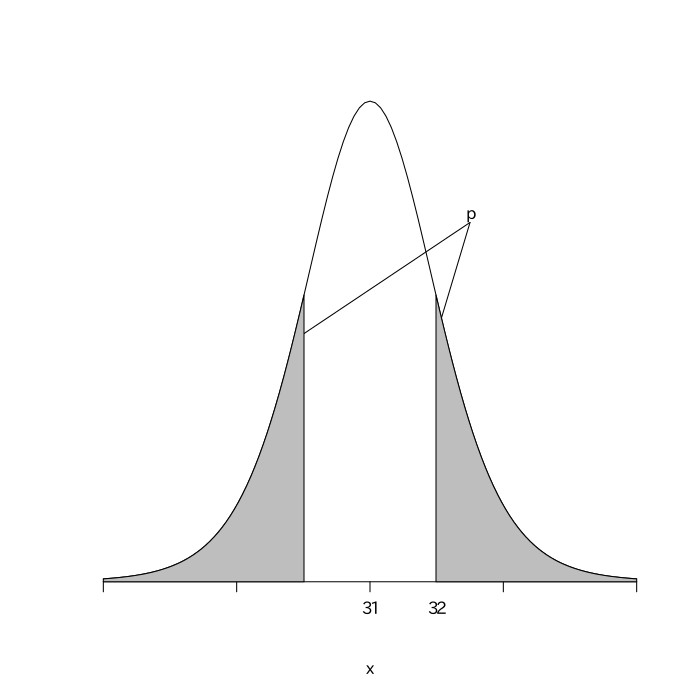
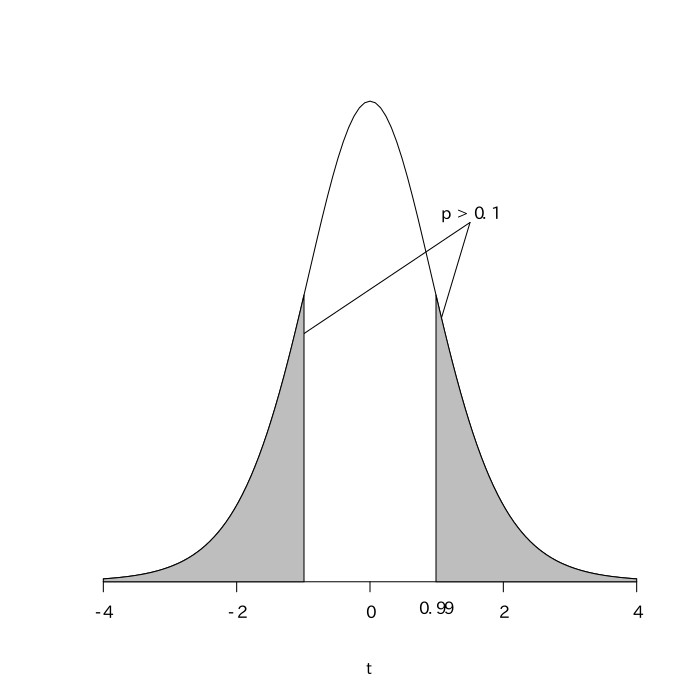
機械を新しくする前と後とでこの工業製品の平均重量は異ならないと仮定する(帰無仮説)。${母集団平均}=31.0$である。標本数が少ないので、$\frac{X-31.0}{\sqrt{\frac{10.24}{10}}}$は自由度が$10{(標本数)}-1=9$のt分布に従う。今、新しい機械で作られたこの工業製品から10個を無作為抽出したものの平均重量が32.0だったので、これをXに代入して計算すると$\frac{32.0-31.0}{\sqrt{1.024}}$
$=\frac{1}{1.012}$
$=0.99$
となる。$t$分布表より自由度が9の$p=0.1$のとき$t=1.83$なので、$t=0.99$はこれより小さく、$p > 0.1$である。
以上より、統計的に、機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたとは言えない。
↓
【問題5】
ある怪しい男が両替屋に金貨を10枚持ってきた。その重さを測定すると、以下の通りであった。この金貨が本物の金貨かどうかを統計的に検定せよ。なお、本物の金貨の平均重量は31.5gである。ただし、この金貨全体の重量は正規分布しているとする。
| 31.36 | 34.33 | 29.18 | 32.81 | 34.15 | 32.75 | 35.31 | 33.23 | 31.67 | 30.69 |
(例題6)
ある工業製品を製造する機械が故障したので、新しい機械に取り替えた。古い機械で作られたその工業製品から5個を無作為抽出して重量を調査したとき、その標本の平均重量は31.0g、その標本の標準偏差は4.4gであった。新しい機械で作られたその工業製品から10個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたと言えるかどうか、統計的に検定せよ。
機械を新しくする前と後とでこの工業製品の平均重量は異ならないと仮定する(帰無仮説)。その平均重量を$\mu$とおく。機械を新しくする前の標本平均の集合を$X_1$とすると、$\frac{X_1-\mu}{\sqrt{3.872}}$は自由度が$5-1=4$の$t$分布に従う。
機械を新しくした後の標本平均の集合を$X_2$とすると、$\frac{X_2-\mu}{\sqrt{1.024}}$は自由度が$10-1=9$の$t$分布に従う。
これらの差$\frac{X_1-X_2}{\sqrt{3.872+1.024}}=\frac{X_1-X_2}{\sqrt{4.896}}$は、自由度が$\frac{(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2})^2}{\frac{s_1^4}{n_1^2(n_1-1)}+\frac{s_2^4}{n_2^2(n_2-1)}}$のt分布に従う(Welchのt検定)。
ここに$X_1=31.0, X_2=32.0$を代入すると
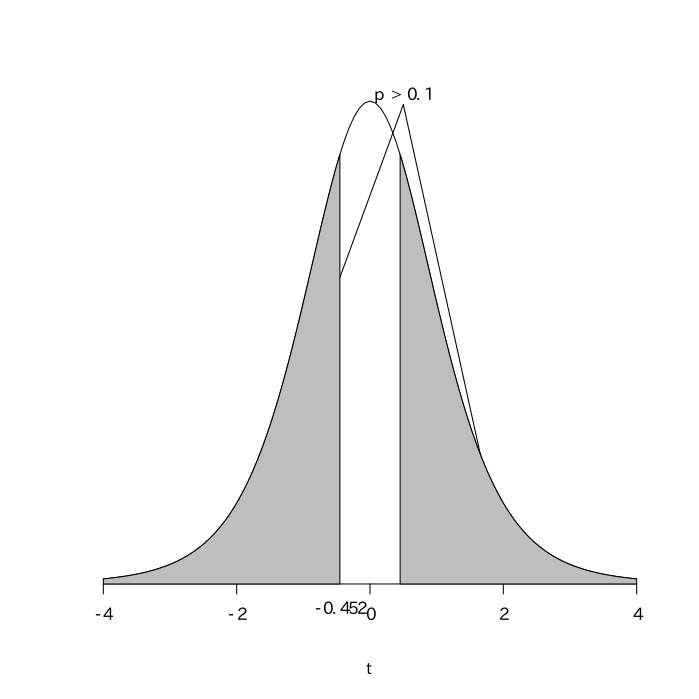
$\frac{-1}{2.213}$ $=-0.452$ となる。
自由度は$n_1=5, s_1=4.4, n_2=10, s_2=3.2$を代入して
$\frac{(\frac{19.36}{5}+\frac{10.24}{10})^2}{\frac{374.8096}{100}+\frac{104.8576}{900}}$
=$\frac{4.896^2}{3.86460444444}$
=$6.20$ となる。
自由度が6のt分布表を読むと$p=0.1$のときの値が$1.943$であり、$t=0.452$のときは$p > 0.1$なので、帰無仮説を棄却できない。
以上より、統計的に、機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたとは言えない。
【問題6】
ある血圧を下げる薬の効果を確かめるために、A群(5人)にはこの薬を投与し、B群(10人)には偽薬を投与して血圧を測定した結果、A群の血圧の平均は110で標準偏差は15、B群の血圧の平均は125で標準偏差は20だった。この薬に血圧を下げる効果があるかどうかを、統計的に検定せよ。
7.4 $\chi^2$検定
(例題7)
ある工業製品の平均重量は31.0g、標準偏差は2.2gであることがわかっている。その工業製品を製造する機械が故障したので、新しい機械に取り替えた。新しい機械で作られたその工業製品から10個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたと言えるかどうか、分散の観点から統計的に検定せよ。
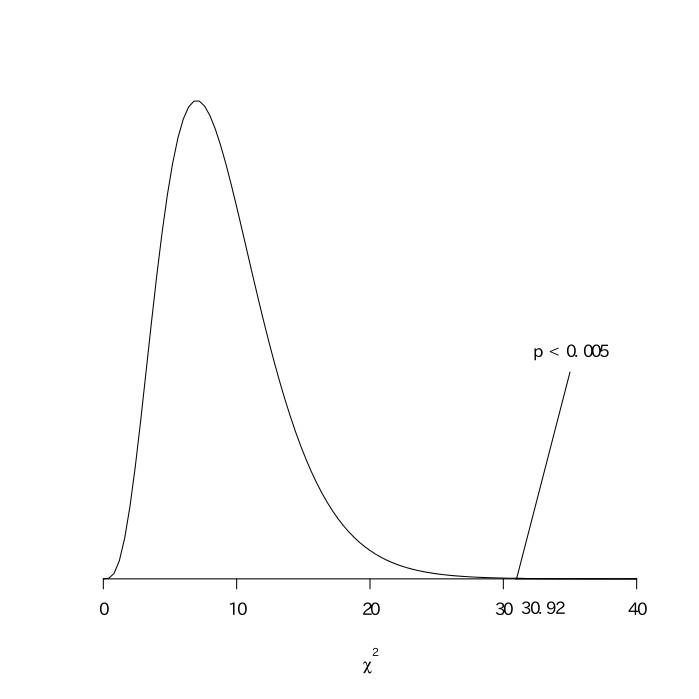
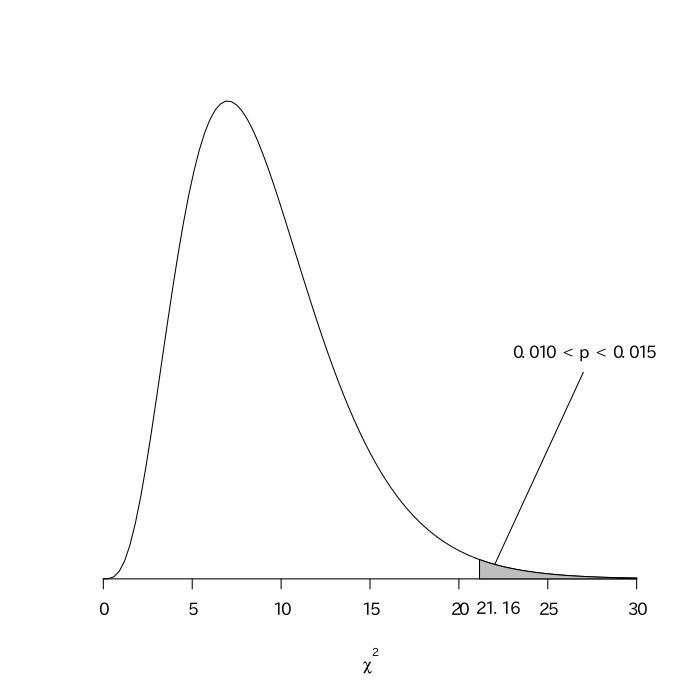
機械を新しくする前と後とでこの工業製品の平均重量は異ならないと仮定する(帰無仮説)。$\frac{ns^2}{\sigma^2}$は自由度が$n-1$の$\chi^2$分布に従う。$\frac{ns^2}{\sigma^2}=\frac{10\times10.24}{2.2^2}=21.16$であり、$\chi^2$分布より自由度が9のところを読むと、$ 0.010 < p < 0.015 $であるので、帰無仮説を棄却できる。
以上より、統計的に、機械を新しくすることでこの工業製品の平均重量に影響をおよぼしたと言える。
【問題7】
ある怪しい男が両替屋に金貨を10枚持ってきた。その重さを測定すると、以下の通りであった。この金貨が本物の金貨かどうかを統計的に検定せよ。なお、本物の金貨の平均重量は31.5g、標準偏差は1gである。
| 31.36 | 34.33 | 29.18 | 32.81 | 34.15 | 32.75 | 35.31 | 33.23 | 31.67 | 30.69 |
(例題8)
あるサイコロを120回振ったときの目の出た回数が次の通りであった。このサイコロが正しく作られているかどうかを統計的に検定せよ。
このサイコロが正しく作られていると仮定する(帰無仮説)。そうすると、それぞれの目が出る回数の期待度数は$120\times\frac16=20$である。その期待度数と実際の値との差を2乗して、その期待度数で割る。その結果を足しあわせたものは、自由度が$6-1=5$の$\chi^2$分布となる。| 目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 回数 | 14 | 27 | 18 | 16 | 22 | 23 |
| 目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 回数 | 14 | 27 | 18 | 16 | 22 | 23 |
| 期待度数 | 20 | 20 | 20 | 20 | 20 | 20 |
| $({回数}-{期待度数})^2$ | 36 | 49 | 4 | 16 | 4 | 9 |
| $\frac{({回数}-{期待度数})^2}{期待度数}$ | 1.8 | 2.45 | 0.2 | 0.8 | 0.2 | 0.45 |
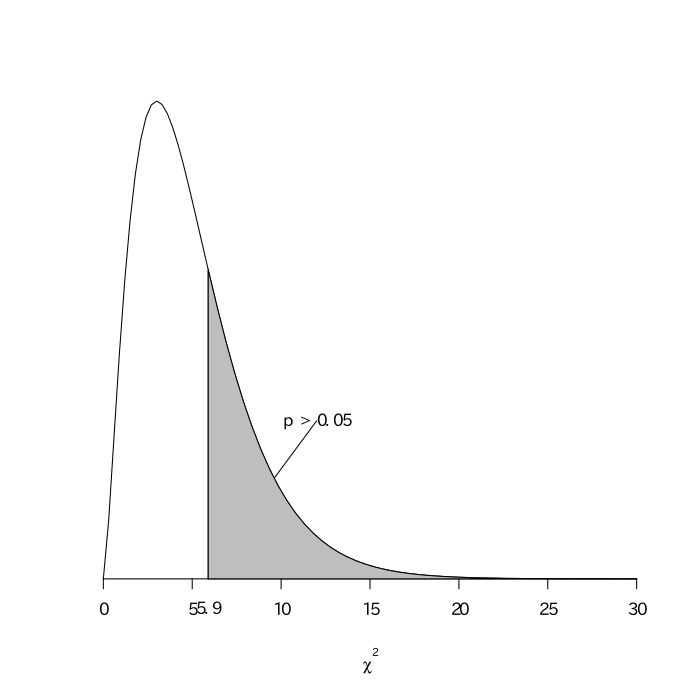
本問では、期待度数と実際の値との差を2乗して、その期待度数で割り、その結果を足しあわせたものが、$1.8+2.45+0.2+0.8+0.2+0.45=5.9$となる。$\chi^2$分布表の自由度が5のところをを読むと、$p=0.05$のときの値が11.075であり、$5.9 < 11.075$から$p > 0.05$となるので、帰無仮説を棄却できない。
以上より、統計的に、このサイコロが正しく作られていないとは言えない。
【問題8】
2014年のプロ野球選手の生まれ月の分布が次の通りであった。生まれ月に偏りがあるかどうかを統計的に検定せよ。
| 生まれ月 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
| 人数 | 60 | 46 | 47 | 103 | 75 | 95 | 103 | 70 | 81 | 76 | 71 | 59 |
- プロ野球選手の2014年の年俸一覧・年俸ランキング・背番号一覧gurazeni.com( http://www.gurazeni.com/ranking/year:2014)より作成
(例題9)
A農園、B農園、C農園で作っているリンゴの品質は次の通りであった。農園と品質との間に関連があるかどうかを統計的に検定せよ。
農園と品質との間に関連がないと仮定する(帰無仮説)。そのときの期待度数は次のようになる。| 優 | 良 | 可 | |
| A農園 | 25 | 62 | 13 |
| B農園 | 70 | 180 | 50 |
| C農園 | 120 | 350 | 130 |
| 優 | 良 | 可 | 計 | |
| A農園 | 21.5 | 59.2 | 19.3 | 100 |
| B農園 | 64.5 | 177.6 | 57.9 | 300 |
| C農園 | 129 | 355.2 | 115.8 | 600 |
| 計 | 215 | 592 | 193 | 1000 |
実際の値と期待度数との差を取って2乗する。
| 優 | 良 | 可 | |
| A農園 | 12.25 | 7.84 | 39.69 |
| B農園 | 30.25 | 5.76 | 62.41 |
| C農園 | 81 | 27.04 | 201.64 |
それを期待度数で割る。
| 優 | 良 | 可 | |
| A農園 | 0.57 | 0.13 | 2.06 |
| B農園 | 0.47 | 0.03 | 1.08 |
| C農園 | 0.63 | 0.08 | 1.74 |
これらを全部足すと
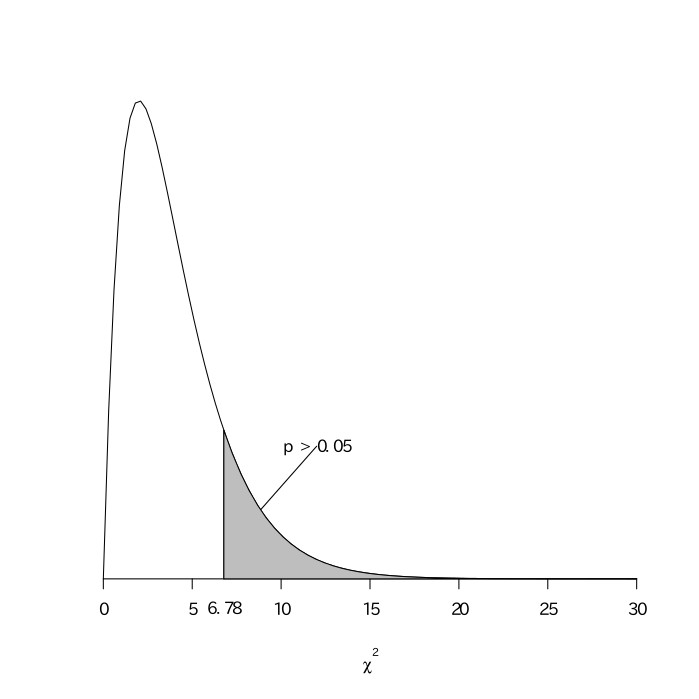
$ 0.57+0.13+2.06+0.47+0.03+1.08+0.63+0.08+1.74=6.78$
これが自由度$(3-1)\times(3-1)=4$の$\chi^2$分布に従うので、$\chi^2$分布表の自由度が4のところをを読むと、$p=0.05$のときの値が9.488であり、$6.78 < 9.488$から$p > 0.05$となるので、帰無仮説を棄却できない。
以上より、統計的に、農園と品質との間に関連があるとは言えない。
【問題9】
内閣府が行っている平成26年国民生活に関する世論調査の中の、「現在の生活に対する満足度」の年齢別回答者数は次の通りであった。年齢と現在の生活に対する満足度との間に関連があるかどうかを統計的に検定せよ。
http://survey.gov-online.go.jp/h26/h26-life/index.html
より。パーセンテージから逆算し、「どちらともいえない」と「わからない」を除外した。
http://survey.gov-online.go.jp/h26/h26-life/index.html
より。パーセンテージから逆算し、「どちらともいえない」と「わからない」を除外した。
| 満足している | まあ満足している | やや不満だ | 不満だ | |
| 20~29歳 | 71 | 274 | 75 | 15 |
| 30~39歳 | 78 | 507 | 197 | 39 |
| 40~49歳 | 81 | 704 | 277 | 61 |
| 50~59歳 | 80 | 622 | 297 | 63 |
| 60~69歳 | 119 | 865 | 334 | 101 |
| 70歳以上 | 165 | 829 | 261 | 93 |