第1章 命題
1.1 集合
(例題1)
大学生 200 人を対象に、飲酒と喫煙に関するアンケートを取った。 その結果、飲酒すると答えた学生は 115 人、喫煙すると答えた学生は 55 人いた。 また、飲酒も喫煙も両方しないと答えた学生は 60 人であった。 このとき、飲酒も喫煙も両方すると答えた学生は何人か。
$A\cup{B}=200-60=140$
$A\cap{B}=(115+55)-140=30$
$A\cap{\overline{B}}=115-30=85$
$\overline{A}\cap{B}=55-30=25$
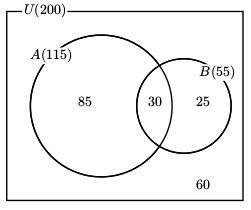
* 問題に答えるだけなら$A\cap{B}=30$だけを求めればよいが、ここでは学習のために他のものもすべて求めた。
【問題1】
総世帯数が200のある地区では、新聞をとっている世帯が170ある。このうちA新聞をとっている世帯は90、B新聞をとっている世帯は120ある。その他の新聞はこの地区にはないものとして、A, B両方の新聞をとっている世帯はいくつか。
1.2 命題
命題の真偽を判定する際には、偽になる反例を探すようにするとよい。もとの命題の真偽と対偶の真偽は一致するが、「逆は必ずしも真ならず」。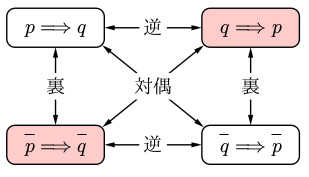
(例題2)
- $△{ABC}$が正三角形ならば、$△{ABC}$は二等辺三角形である。
- $ab$が偶数ならば、$a$も$b$も偶数である。
- $x^2$が4の倍数でなければ、$x$は4の倍数でない。
- ベン図で考える
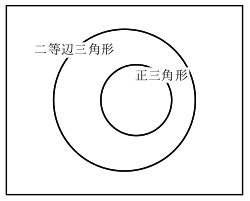
図より、この命題は真である。 - $a=3, b=4$だとすると、$ab=12$と偶数になるが、$a$は偶数ではない。よってこの命題は偽である。
- この命題の対偶は、「$x$が4の倍数であれば、$x^2$は4の倍数である」である。$x=4k$($k$は整数)とすると、$x^2=16k^2$となり、4の倍数となる。よってこの命題は真である。
【問題2】
- $△{ABC}$が正三角形ならば、$△{ABC}$は直角三角形である。
- $x$が4の倍数でなければ、$x^2$は4の倍数でない。
- $x^2\ne9$ならば、$x\ne3$である。
【問題3】
4枚のカードがあり、それぞれ片面にはアルファベットが、もう片面には数字が書かれている。このとき、A, F, 4, 7のカードがあり、「片面が母音ならば、そのカードの裏は偶数でなければならない」というルールが成立しているかどうかを確かめたい。少なくとも、どのカードを調べる(引っくり返してみる)必要があるか。
1.3 必要条件・十分条件
「$p$ならば$q$」の命題が真のとき、$p$は$q$の十分条件、$q$は$p$の必要条件である。(例題3)
次の文の空所に、「必要」「十分」「必要十分」のいずれかを入れなさい。
- 動物であることは、犬であるための( )条件である。
- ソクラテスであることは、人間であるための( )条件である。
- 4つの角が直角であることは、四辺形が長方形であるための( )条件である。
- 「動物であるならば、犬である」は偽、「犬であるならば、動物である」は真なので、必要条件である。
- 「ソクラテスであるならば、人間である」は真、「人間であるならば、ソクラテスである」は偽なので、十分条件である。
- 「4つの角が直角ならば、四辺形が長方形である」は真、「四辺形が長方形ならば、4つの角は直角である」は真なので、必要十分条件である。
【問題4】
- ぶどうであることは、果物であることの( )条件である。
- 哺乳類であることは、動物であることの( )条件である。
- 得点が失点を上回っていることは、野球の試合に勝つことの( )条件である。
(例題4)
それぞれ一つの NPOで活動しているA~Eの5人がいる。5人のうち4人は同じNPOで活動し 1人だけ異なる NPOで活動している。5人がそれぞれ所属している NPOの月々の活動について次のことが分かっているとき 1人だけ異なる NPOに所属しているのは誰か。
分かっていることを次のように記号化する。
- Aが所属している NPOでは 理事会がない月には 清掃活動も教育支援活動も行わない。
- Bが所属している NPOでは 清掃活動と教育支援活動の両方を行う月には 理事会もある。
- Cが所属している NPOでは 理事会がない月には 清掃活動と教育支援活動の少なくとも一方を行わない。
- Dが所属している NPOでは 清掃活動と教育支援活動の少なくとも一方を行う月には 理事会もある。
- Eが所属している NPOでは 理事会がない月には 清掃活動か教育支援活動のどちらか一方を行い他方は行わない。
- A
- B
- C
- D
- E
- $\overline{り} \Rightarrow \overline{せ}\cap\overline{き}$
- ${せ}\cap{き} \Rightarrow {り}$
- $\overline{り} \Rightarrow \overline{せ}\cup\overline{き}$
- ${せ}\cup{き} \Rightarrow {り}$
- $\overline{り} \Rightarrow ({せ}\cap\overline{き})\cup(\overline{せ}\cap{き})$
- ${せ}\cup{き} \Rightarrow {り}$
- $\overline{り} \Rightarrow \overline{せ}\cup\overline{き}$
- ${せ}\cap{き} \Rightarrow {り}$
- $\overline{り} \Rightarrow \overline{せ}\cap\overline{き}$
- $(\overline{{せ}\cap\overline{き}})\cap(\overline{\overline{せ}\cap{き}}) \Rightarrow {り}$
【問題5】
ある会社において、自分の好みの食事に関するアンケート調査を行ったところ、A、B、Cのことが分かった。これから確実にいえるのはどれか。ただし、どの食事も少なくとも1人は好きな食事として回答した人がいた。
- ラーメンとすしが好きな人は、カレーライスも好きである。
- ラーメンも焼肉も好きでない人は、すしかピザが好きである。
- 焼肉が好きな人は、カレーライスもピザも好きではない。
- カレーライスが好きな人は、焼肉が好きである。
- ラーメンが好きな人は、焼肉が好きである。
- すしが好きでない人は、ラーメンも焼肉も好きである。
- ピザが好きな人は、焼肉が好きではない。
- ラーメンが好きな人は、カレーライスが好きである。
