第２章 場合の数
場合の数（全部で何通りか）を考えるときには、数え上げるのが基本。辞書式配列や樹形図が有効であり、計算で求めることができる場合もある。（例題１）
A, B, C, Dの４人を一列に並べる方法は何通りあるか
（ア）辞書式配列で考える
- ABCD
- ABDC
- ACBD
- ACDB
- ADBC
- ADCB
- BACD
- BADC
- BCAD
- BCDA
- BDAC
- BDCA
- CABD
- CADB
- CBAD
- CBDA
- CDAB
- CDBA
- DABC
- DACB
- DBAC
- DBCA
- DCAB
- DCBA
（イ）樹形図で考える
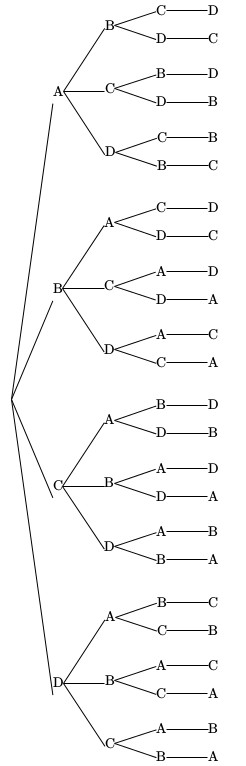
以上より24通り
（ウ）計算で求める。
（樹形図を思い浮かべながら）
$4\times3\times2\times1=24$
以上より24通り
＊ これを$_4P_4$や$4!$と表すことがある。
【問題１】
A, B, C, D, Eの５人を一列に並べる方法は何通りあるか。
（例題２）
A, B, C, D, E, F, Gの7人のうち3人を一列に並べる方法は何通りあるか。
（樹形図を想像しながら）$7\times6\times5=210$
以上より210通り。
＊ これを$_7P_3$と表すことがある。
（例題３）
A, B, C, D, E, F, Gの7人から委員長、副委員長、書記を選ぶ方法は何通りあるか。
7人のうち3人を一列に並べて先頭から順に委員長、副委員長、書記であると考えると$7\times6\times5=210$
以上より210通り。
（例題４）
A, B, C, D, E, F, Gの7人から3人の委員を選ぶ方法は何通りあるか。
仮にA, B, Cの3人が委員に選ばれたとして、その中で委員長、副委員長、書記の役職を割り振る方法は、その3人を一列に並べて先頭から順に委員長、副委員長、書記であると考えると$3\times2\times1=6$通りである。どの3人が選ばれても同様に考えることができるので、求める総数は$210\div6=35$通り。
＊ これを$_7C_3=\frac{_7P_3}{_3P_3}$と表すことがある。
【問題２】
A, B, C, D, E, F, G, H, I, Jの10人から4人の委員を選ぶ方法は何通りあるか。
（例題５）
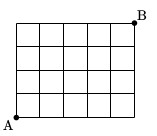右のような道があるとき、AからBまでの最短経路は何通りあるか。
右へ進むことを→、上へ進むことを↑と表すと、例えば１つの最短経路は以下のように表すことができる。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
| → | → | ↑ | ↑ | → | ↑ | → | → | ↑ |
↑に着目すると、この例は(3), (4), (6), (9)と表すことができる。
求める総数は、このようにして、(1)〜(9)に→を5回、↑を4回配置する総数、つまり、(1)〜(9)の9つから↑が配置される4つを選ぶ総数なので、$(9\times8\times7\times6)\div(4\times3\times2\times1)=126$通りである。
【問題３】
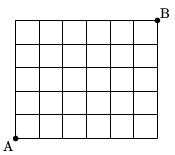右のような道があるとき、AからBまでの最短経路は何通りあるか。
