第4章 記述統計
4.1 グラフ
(例題1)
以下のグラフをもとにして、団塊の世代に属するあるコメンテーターが「少年による凶悪犯罪が近年急増している。私たちと違って今どきの子どもはキレやすい。」と言っている。これは正しいか。
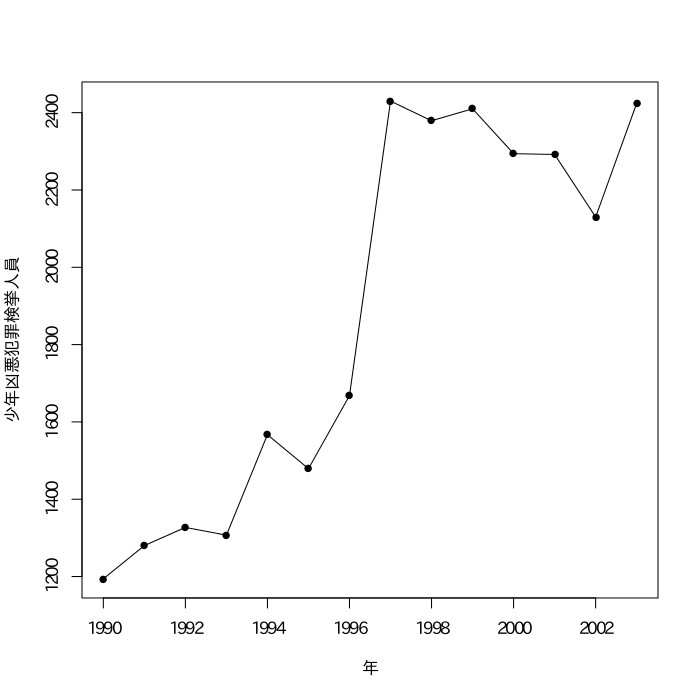
正しくない。上のグラフは一部だけを切り取っている。1946年〜2013年までの図は次の通りである。
- 平成26年版 犯罪白書(http://hakusyo1.moj.go.jp/jp/61/nfm/mokuji.html)「資料3-3 少年による刑法犯 検挙人員(罪名別)」より作成。
- 「凶悪犯罪」とは殺人、強盗、強姦、放火の合計である。
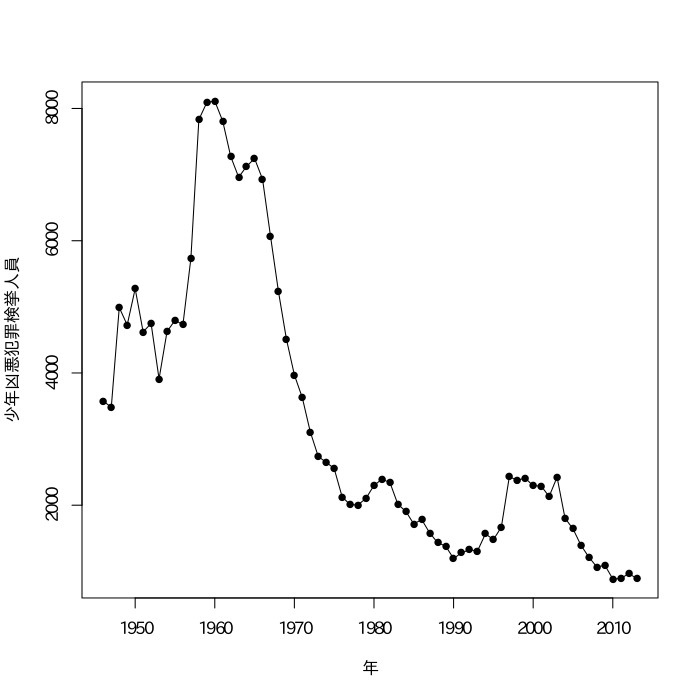
なお、人口比についても同様の傾向である。
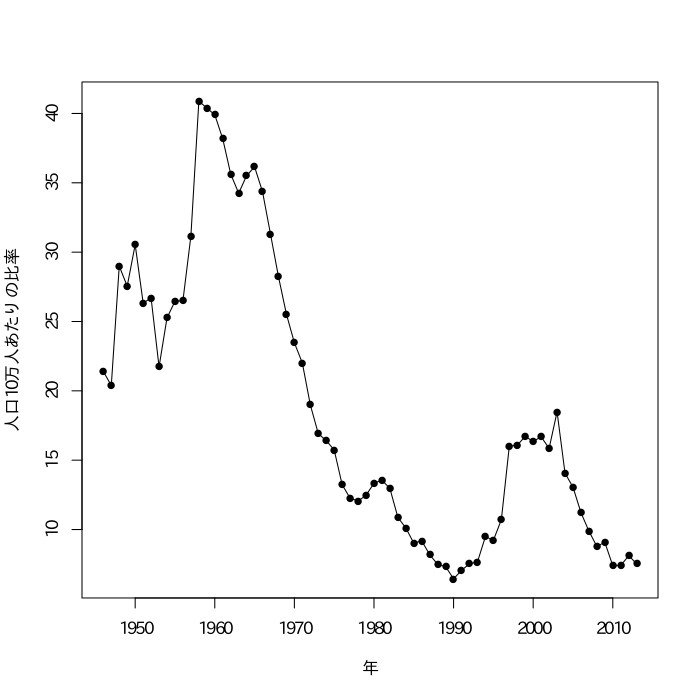
【問題1】
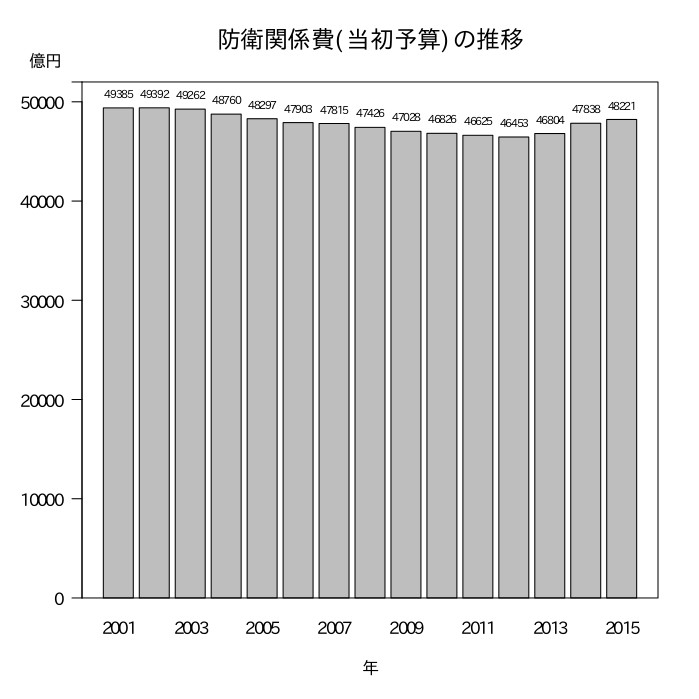
以下のグラフをもとにして、ある政治評論家が「日本の防衛関係費は2000年から2012年にかけて急速に縮小していたが、第二次安倍内閣が発足した2012年からはすごい勢いで増えている。」と言っている。これは正しいか。
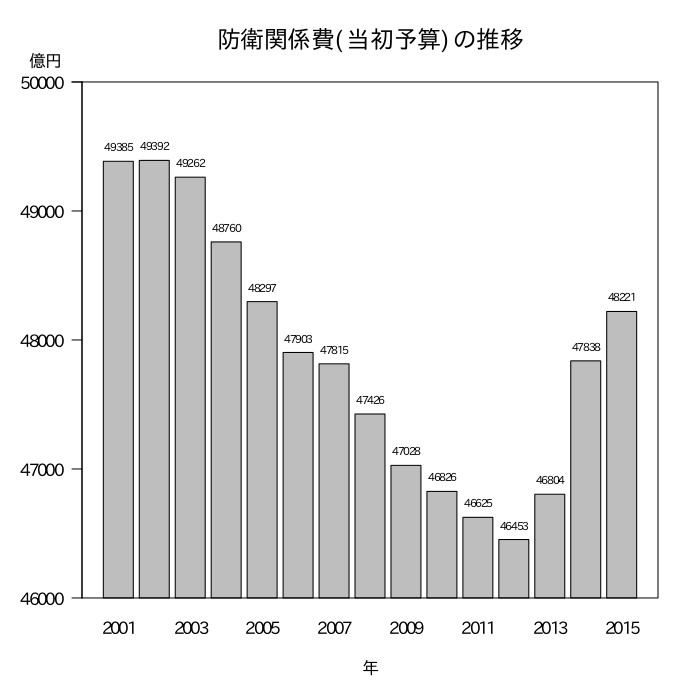

- 平成27年版 防衛白書(http://www.mod.go.jp/j/publication/wp/wp2015/w2015_00.html)「巻末資料4 過去15年間の防衛関係費(当初予算)の推移」より作成。
4.2 代表値
(例題2)
以下の度数分布表とヒストグラムを見て、平均値、中央値、最頻値のうちのどれがデータを代表する値としてふさわしいか答えよ。

国内での分布は問わず一国全体を大まかに捉えるのなら平均値が適していると考えられる。ちょうど真ん中の順位の世帯の所得を知りたければ中央値が適している。どの区分の所得の世帯が最も多いかという観点からは最頻値が適している。
| 階級 | 度数(世帯数) |
| 0〜100 | 3328446 |
| 100〜200 | 7009909 |
| 200〜300 | 7211633 |
| 300〜400 | 6757754 |
| 400〜500 | 5093531 |
| 500〜600 | 4286635 |
| 600〜700 | 3479739 |
| 700〜800 | 3227584 |
| 800〜900 | 2521550 |
| 900〜1000 | 1865947 |
| 1000〜1100 | 1412068 |
| 1100〜1200 | 1109482 |
| 1200〜1300 | 756465 |
| 1300〜1400 | 504310 |
| 1400〜1500 | 353017 |
| 1500〜1600 | 252155 |
| 1600〜1700 | 252155 |
| 1700〜1800 | 151293 |
| 1800〜1900 | 201724 |
| 1900〜2000 | 100862 |
| 2000〜 | 605172 |
- 平成26年 国民生活基礎調査の概況(http://www.mhlw.go.jp/toukei/saikin/hw/k-tyosa/k-tyosa14/)「Ⅱ 各種世帯の所得等の状況 」より作成。
- 度数については割合から逆算したので誤差があると思われる。
【問題2】
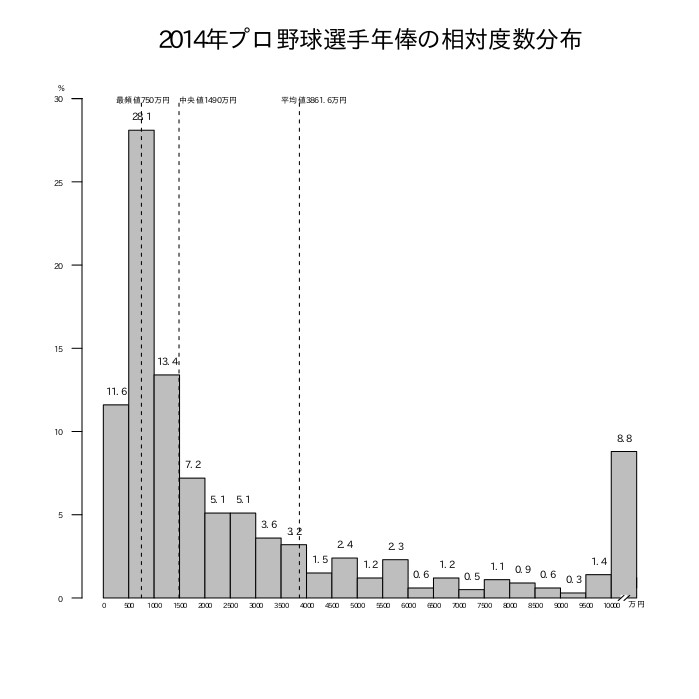
以下の2014年プロ野球選手年俸の生データ(一部のみ抜粋)から度数分布表とヒストグラムを作成して、平均値、中央値、最頻値を求め、そのうちのどれがデータを代表する値としてふさわしいか答えよ。
| # | 背番号 | 選手 | 年俸(推定) | チーム | ポジション | 投打 | 生年月日 |
| 1 | 10 | 阿部 慎之助 | 6億円 | 巨人 | 内野手 | 右投げ 左打ち | 1979年 3月 20日 |
| 2 | 18 | 杉内 俊哉 | 5億円 | 巨人 | 投手 | 左投げ 左打ち | 1980年 10月 30日 |
| 3 | 20 | ケビン・ユーキリス | 4億円 | 楽天 | 内野手 | 右投げ 右打ち | 1979年 3月 15日 |
| $\vdots$ |
- プロ野球選手の2014年の年俸一覧・年俸ランキング・背番号一覧gurazeni.com( http://www.gurazeni.com/ranking/year:2014)より引用
(例題3)
30年後に1万ドルが償還される割引債(ゼロクーポン債)の米国債が2000ドルで売りだされている。この米国債の1年あたりの平均利率を求めよ。
$10000\div2000=5$より、この米国債を買うと30年で5倍(500%)になる。つまり、400%増加する。$400\div30\fallingdotseq13.3$であるが、これは1年あたりの平均利率ではない(単利で考えたときの平均利回りだとは言える)。
正しくは、$(x)^{30}=5$を解いて$x\fallingdotseq1.055$より、5.5%である。
【問題3】
ニューヨークのマンハッタン島は、1626年に、オランダ人入植者がアメリカ先住民から24ドルで買ったと言われている。この価格について、AさんとBさんは次のように考えた。どちらの考え方が正しいか。
- 1626年から2015年現在まで389年経っている。$5%\times389=1945%$なので、当時の24ドルが現在までに1945%増加して、$24+24\times19.45=490.8$ドルになると考えられる。マンハッタン島が$490.8$ドルというのは安いと考えられる。
- 1626年から2015年現在まで389年経っている。$(1.05)^{389}\fallingdotseq174838607$なので、当時の24ドルが現在までに$24\times174838607=4196126568$ドルになると考えられる。マンハッタン島が約42億ドルというのはそれなりに妥当な価格であると考えられる。
4.3 分散と標準偏差
(例題4)
以下はA〜Jの10人が受けたテストの結果である。国語の点数の分散と標準偏差を求めよ。
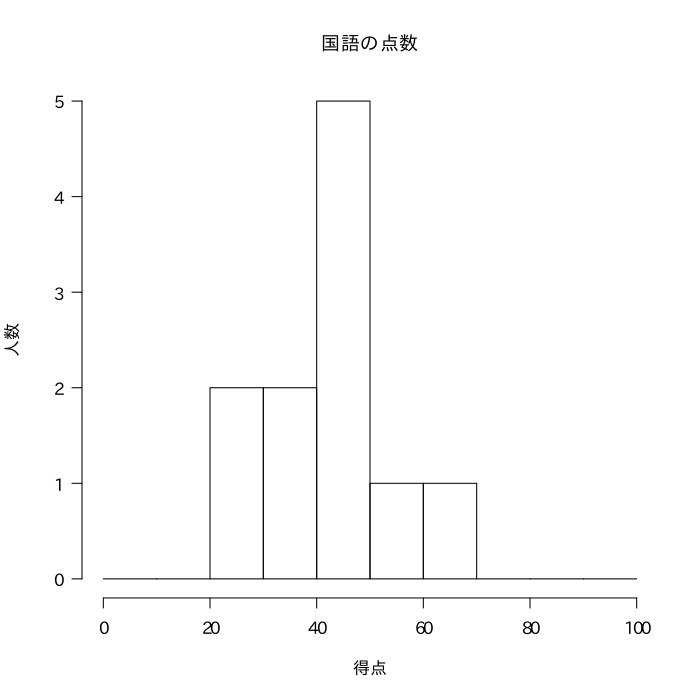
| 科目 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 国語 | 40 | 35 | 65 | 50 | 30 | 45 | 60 | 45 | 50 | 30 | 45 |

| 科目 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 国語 | 40 | 35 | 65 | 50 | 30 | 45 | 60 | 45 | 50 | 30 | 45 |
| 国語$-$平均 | $-5$ | $-10$ | 20 | 5 | $-15$ | 0 | 15 | 0 | 5 | $-15$ | 0 |
| (国語$-$平均)$^2$ | $25$ | $100$ | 400 | 25 | $225$ | 0 | 225 | 0 | 25 | $225$ | 0 |
分散$=\frac{25+100+400+25+225+0+225+0+25+225}{10}=125$
標準偏差$=\sqrt{125}\fallingdotseq11.2$
【問題4】
以下はA〜Jの10人が受けたテストの結果である。数学の点数の分散と標準偏差を求めよ。

| 科目 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 数学 | 20 | 15 | 90 | 70 | 5 | 25 | 100 | 35 | 85 | 5 | 45 |

(例題5)
平成26年センター試験の国語で200点満点を取ったときの偏差値を求めよ。ただし、同試験の平均点は98.67、標準偏差は26.83である。
http://www.dnc.ac.jp/sp/data/shiken_jouhou/h26/index.htmlより
偏差値は、平均点が50、$\pm$1標準偏差で$\pm$10になるように作られた指標である。よって求める偏差値はhttp://www.dnc.ac.jp/sp/data/shiken_jouhou/h26/index.htmlより
$50+\frac{200-98.67}{26.83}\times10\fallingdotseq87.8$
なお、得点の分布は
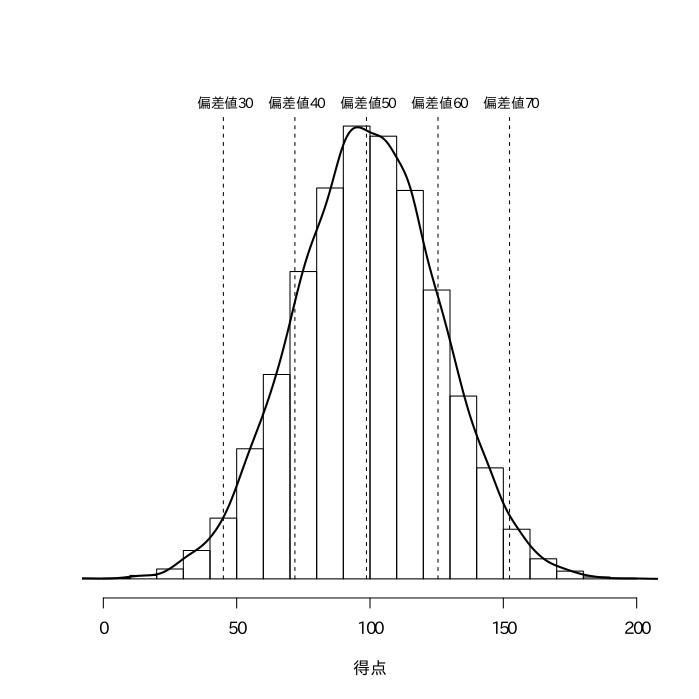 のようなものかもしれないし、
のようなものかもしれないし、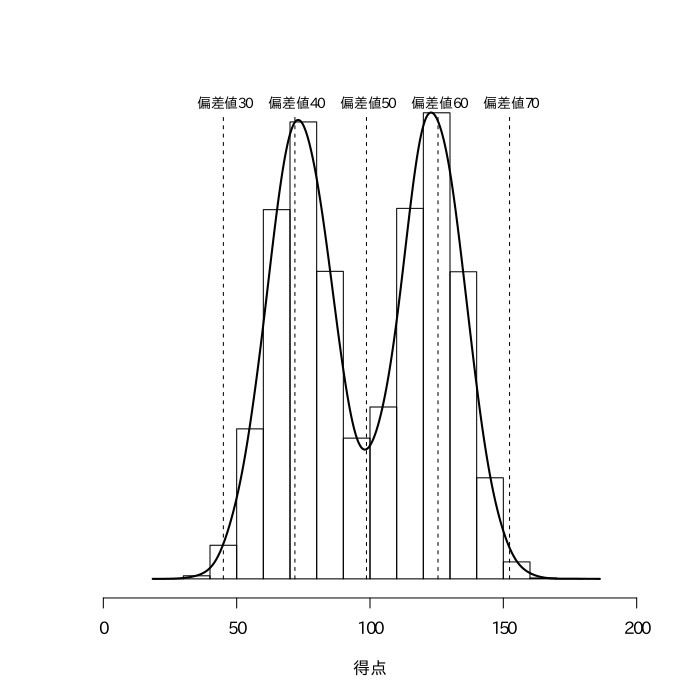 のようなものかもしれない。
のようなものかもしれない。【問題5】
平成26年センター試験の数学2Bで100点満点を取ったときの偏差値を求めよ。ただし、同試験の平均点は53.94、標準偏差は23.02である。
4.4 相関関係
(例題6)
以下はA〜Jの10人が受けたテストの結果である。国語の点数と数学の点数の相関係数を求めよ。
| 科目 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 国語 | 40 | 35 | 65 | 50 | 30 | 45 | 60 | 45 | 50 | 30 | 45 |
| 数学 | 20 | 15 | 90 | 70 | 5 | 25 | 100 | 35 | 85 | 5 | 45 |
| 科目 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 国語 | 40 | 35 | 65 | 50 | 30 | 45 | 60 | 45 | 50 | 30 | 45 |
| 数学 | 20 | 15 | 90 | 70 | 5 | 25 | 100 | 35 | 85 | 5 | 45 |
| 国語$-$平均 | $-5$ | $-10$ | 20 | 5 | $-15$ | 0 | 15 | 0 | 5 | $-15$ | 0 |
| 数学$-$平均 | $-25$ | $-30$ | 45 | 25 | $-40$ | $-20$ | 55 | $-10$ | 40 | $-40$ | 0 |
共分散$=\frac{(-5)\cdot(-25)+(-10)\cdot(-30)+20\cdot45+5\cdot25+(-15)\cdot(-40)+0\cdot(-20)+15\cdot55+0\cdot(-10)+5\cdot40+(-15)\cdot(-40)}{10}=367.5$
相関係数$=\frac{共分散}{{国語の標準偏差}\cdot{数学の標準偏差}}=\frac{367.5}{11.2\cdot35.4}\fallingdotseq0.93$
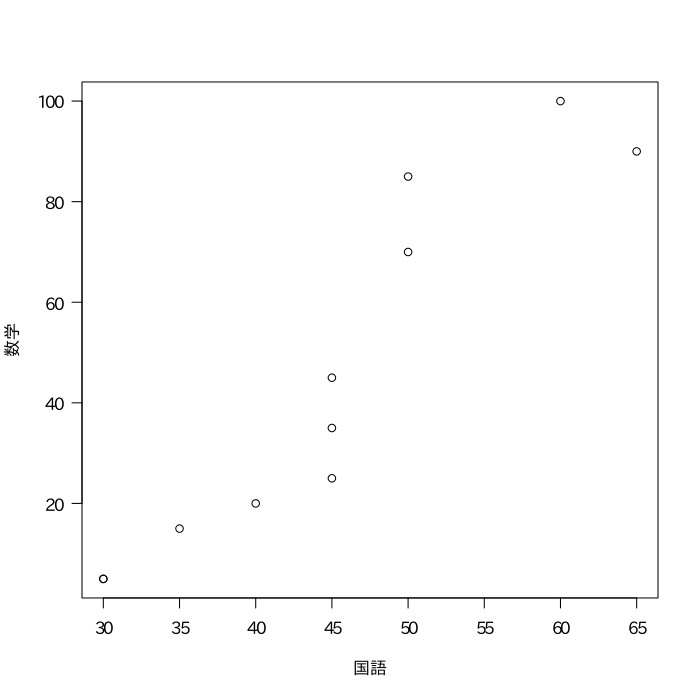
【問題6】
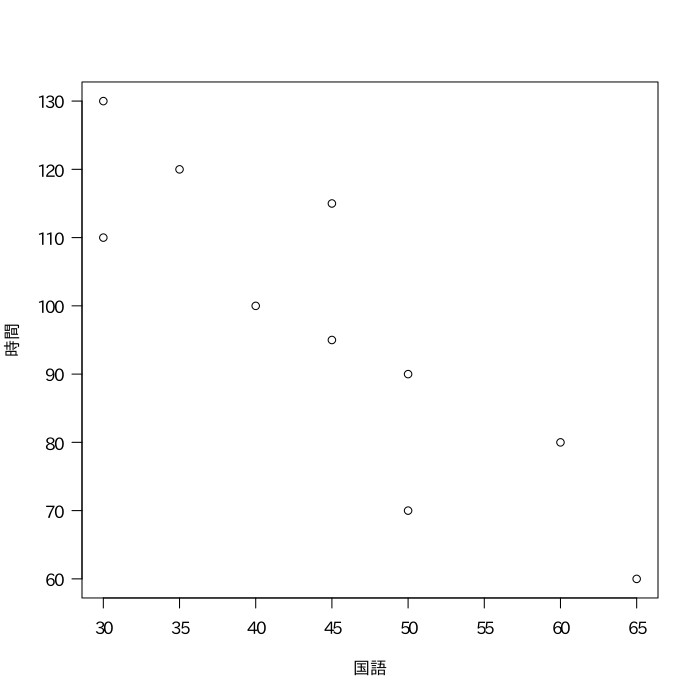
以下はA〜Jの10人が受けたテストの結果とある1500語の文章を読むのにかかった時間である。国語の点数とある1500語の文章を読むのにかかった時間との相関係数を求めよ。
| 科目 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 国語 | 40 | 35 | 65 | 50 | 30 | 45 | 60 | 45 | 50 | 30 | 45 |
| 時間 | 100 | 120 | 60 | 70 | 130 | 115 | 80 | 95 | 90 | 110 | 97 |
【問題7】
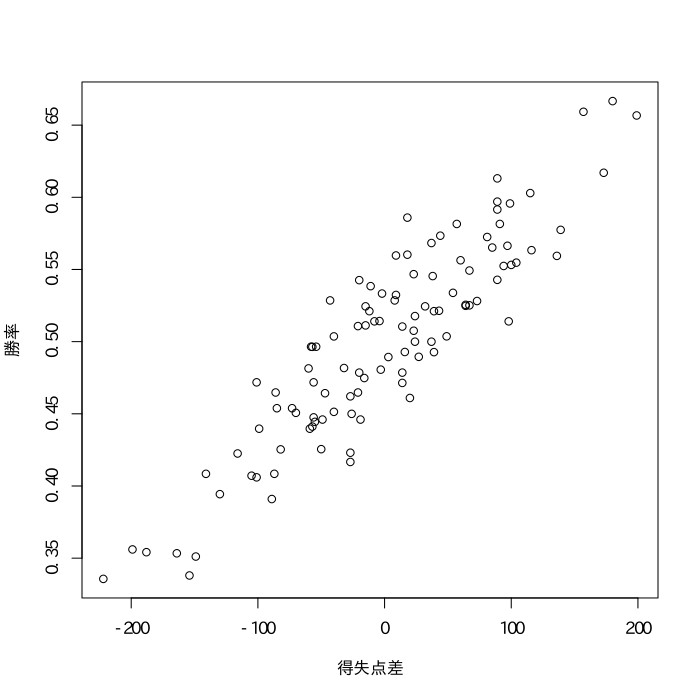
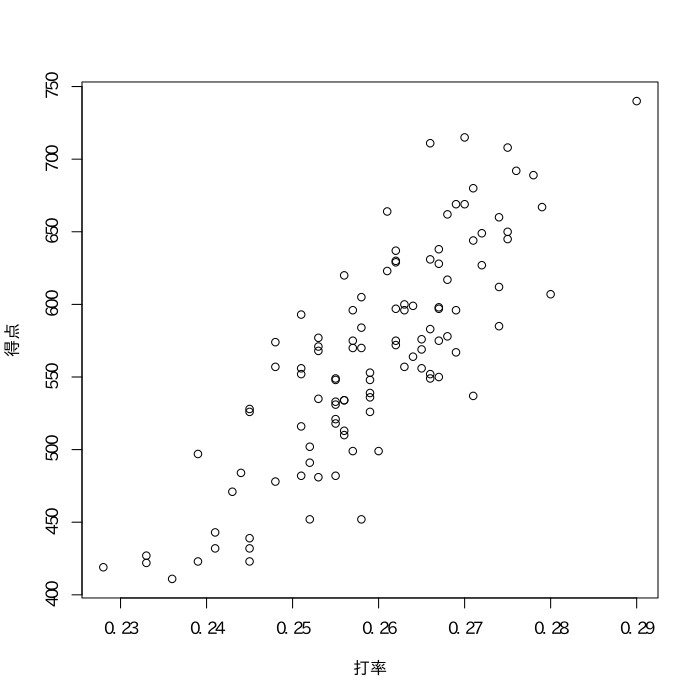
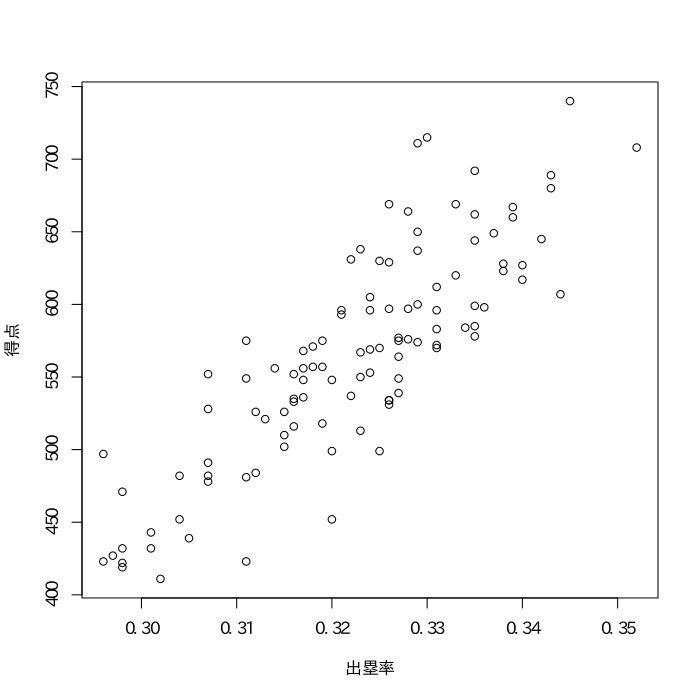
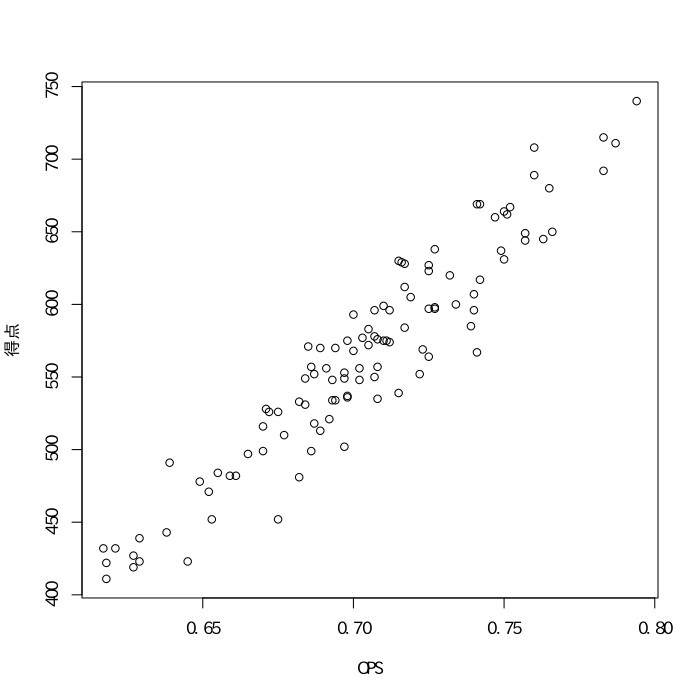
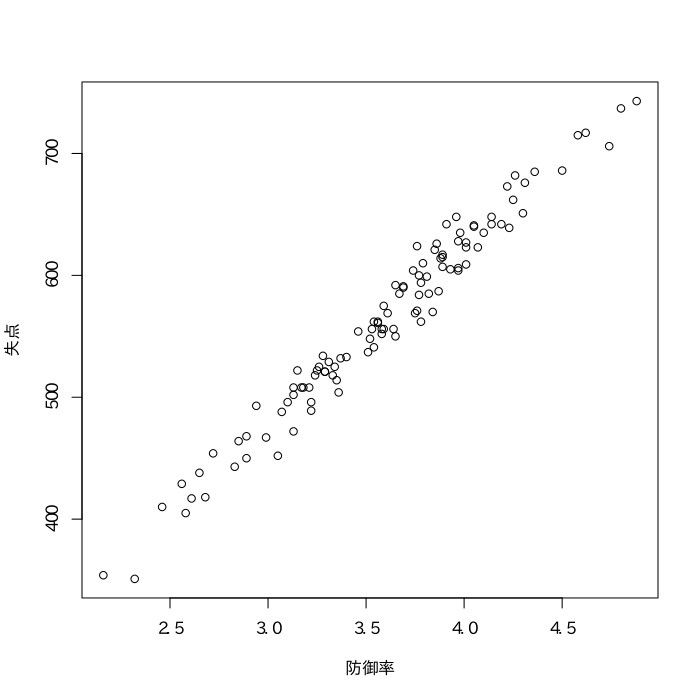
以下の2006年〜2014年の日本プロ野球チームのデータをもとにして、得失点差と勝率、打率と得点、出塁率と得点、OPSと得点、防御率と失点の相関係数を求めよ。
* OPS$={出塁率}+{長打率}$である。
長打率$=\frac{{単打}\times1+{二塁打}\times2+{三塁打}\times3+{本塁打}\times4}{打数}$である。
| 年度 | チーム | 打率 | 出塁率 | OPS | 防御率 | 得点 | 失点 | 勝 | 敗 |
| 2006 | D | 0.270 | 0.333 | 0.742 | 3.10 | 669 | 496 | 87 | 54 |
| 2006 | T | 0.267 | 0.328 | 0.725 | 3.13 | 597 | 508 | 84 | 58 |
| $\vdots$ | |||||||||
| 2014 | L | 0.248 | 0.329 | 0.712 | 3.77 | 574 | 600 | 63 | 77 |
| 2014 | E | 0.255 | 0.327 | 0.684 | 3.97 | 549 | 604 | 64 | 80 |
* OPS$={出塁率}+{長打率}$である。
長打率$=\frac{{単打}\times1+{二塁打}\times2+{三塁打}\times3+{本塁打}\times4}{打数}$である。
- プロ野球 ヌルデータ置き場 - Ver2.0 - 2015年度版(http://lcom.sakura.ne.jp/NulData/)より作成
(例題7)
ある店の傘立てに差してある傘の本数とその日のその場所での雨量との相関係数を計算すると0.9であった。このことから、「傘立てに傘を多く差すと雨が多く降る」と言ってよいか。
よくない。相関関係と因果関係は異なる。ここでは逆に、雨が多く降ると傘立てに差される傘の本数が多くなるという因果関係が想定される。【問題8】
病院の規模とその病院患者の死亡率との相関係数を計算すると0.8であった。このことから、「規模の大きな病院ほど治療が悪くて死亡率が高くなる」と言ってよいか。
(例題8)
ある国において、アイスクリームの売上と水死者数との相関係数を計算すると0.8であった。このことから、「アイスクリームが水死を引き起こす」と言ってよいか。
よくない。相関関係と因果関係は異なる。ここでは気温の高さという第三の要因が、アイスクリームの売上と水死者数の両方を増加させていると考えられる。【問題9】
海賊の数と世界の平均気温との相関係数を計算すると$-0.8$であった。このことから「海賊が地球温暖化を防いでいた(海賊が減ったせいで地球温暖化になった)」と言ってよいか。