第6章 推測統計(推定)
6.1 推定の考え方
(例題1)
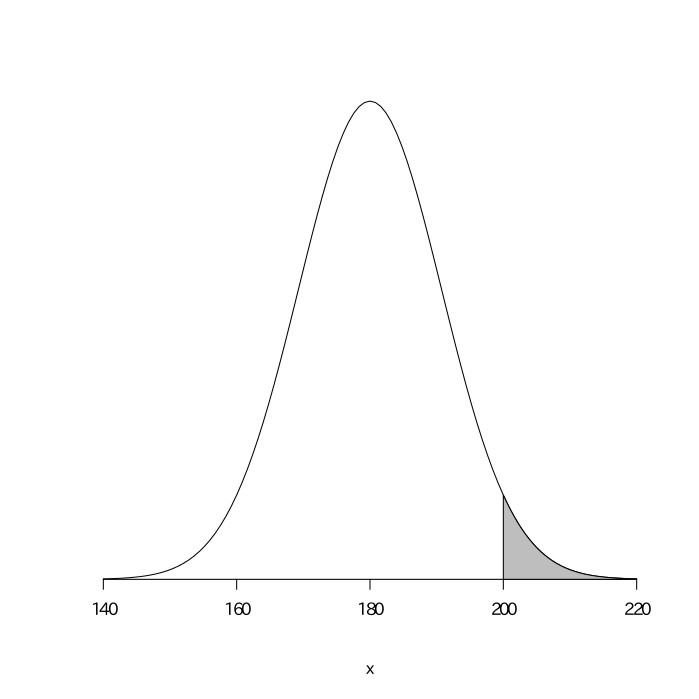
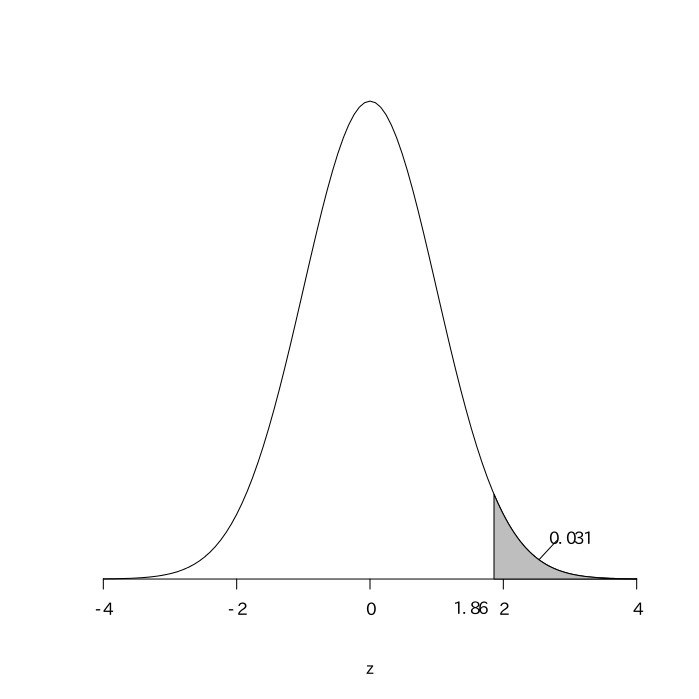
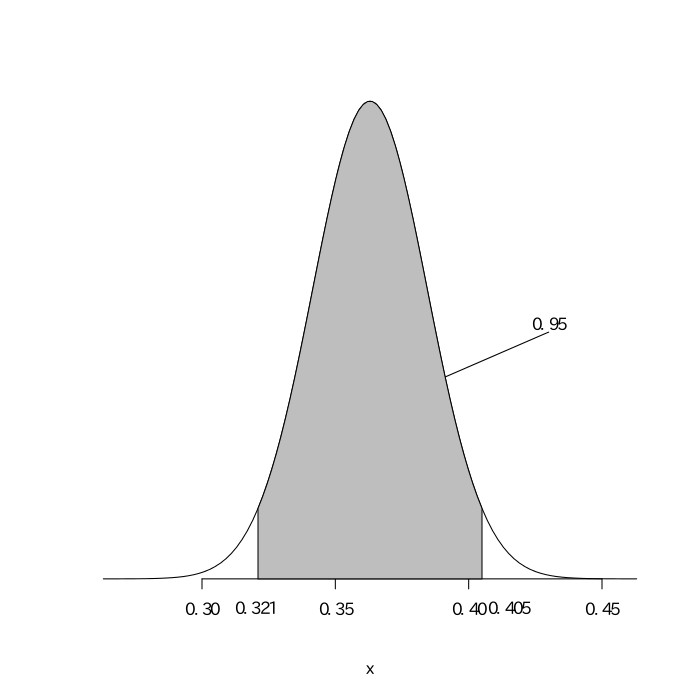
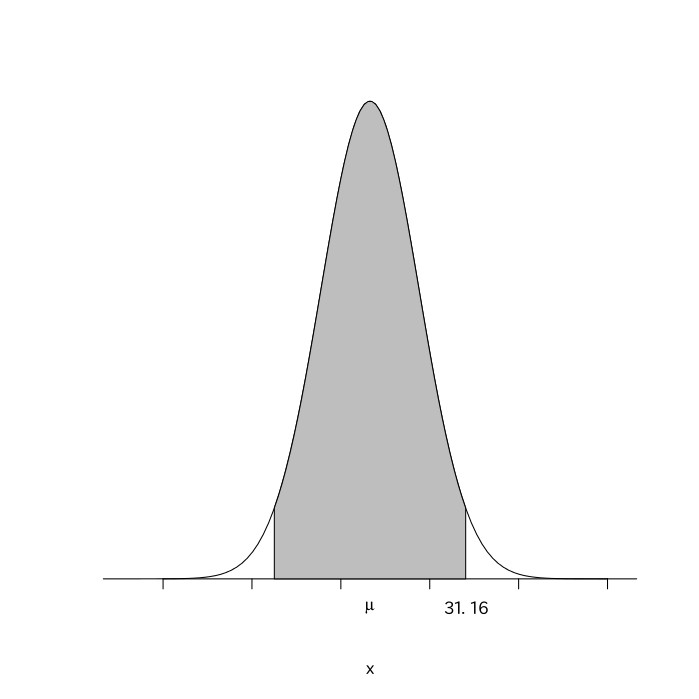
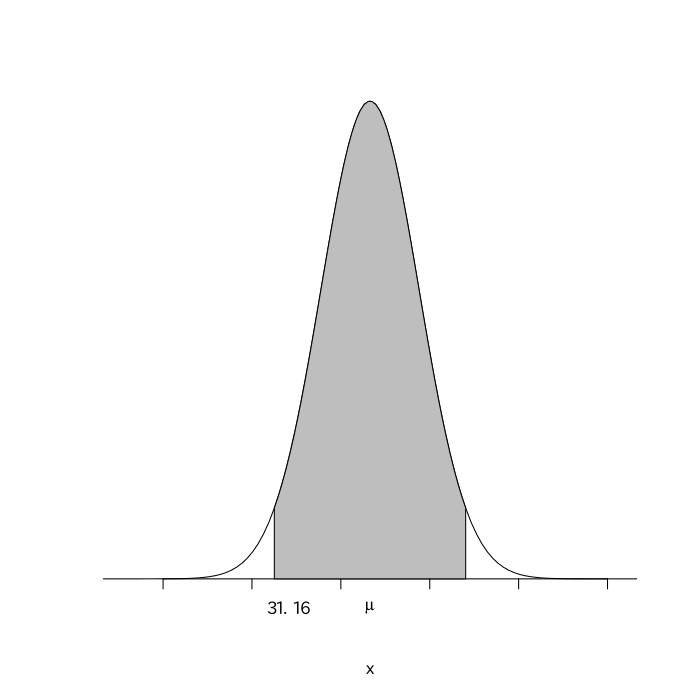
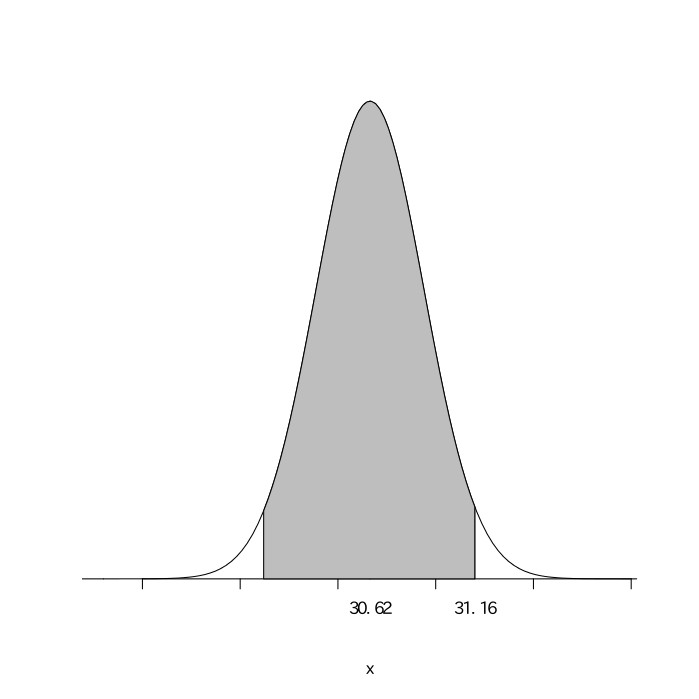
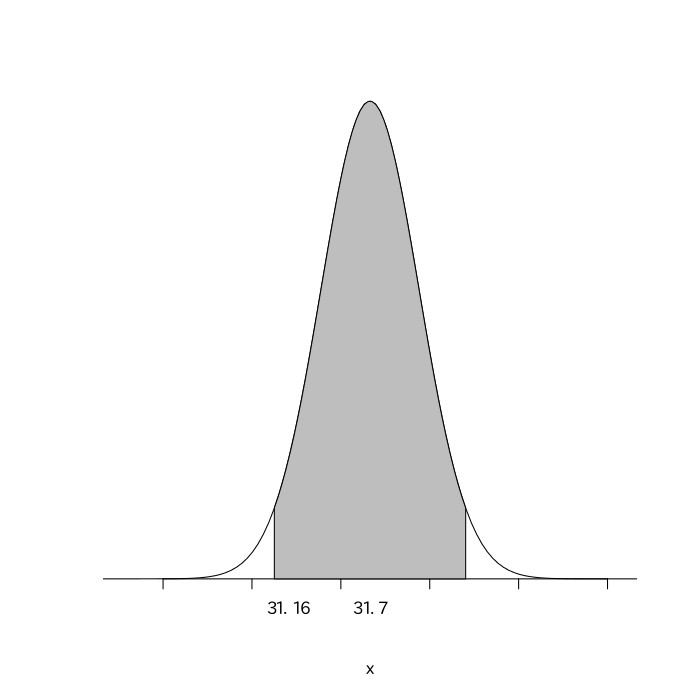
次の図のように、0.35の割合で当たりとなるルーレットがある。500回このルーレットを回したときに、200回以上当たる確率を求めよ(標準正規分布表は与えられているものとする)。
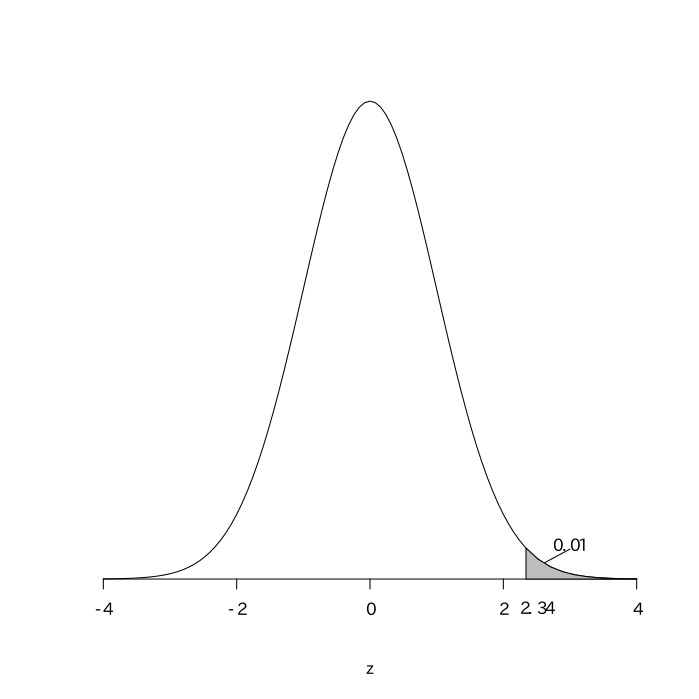
これは$(500, 0.35)$の二項分布になるので、平均が$500\times0.35=175$、分散が$500\times0.35\times(1-0.35)=113.75$の正規分布となる。この当たる回数を$X$とすると、$\frac{X-175}{\sqrt{113.75}}$は平均が0、分散が1の標準正規分布になる。その式に$X=200$を代入すると、$\frac{200-175}{\sqrt{113.75}}\fallingdotseq2.34$となり、$z=2.34$のところの値を標準正規分布表で読み取ると$.490$である。よって求める確率は$0.5-0.490=0.01$となる。
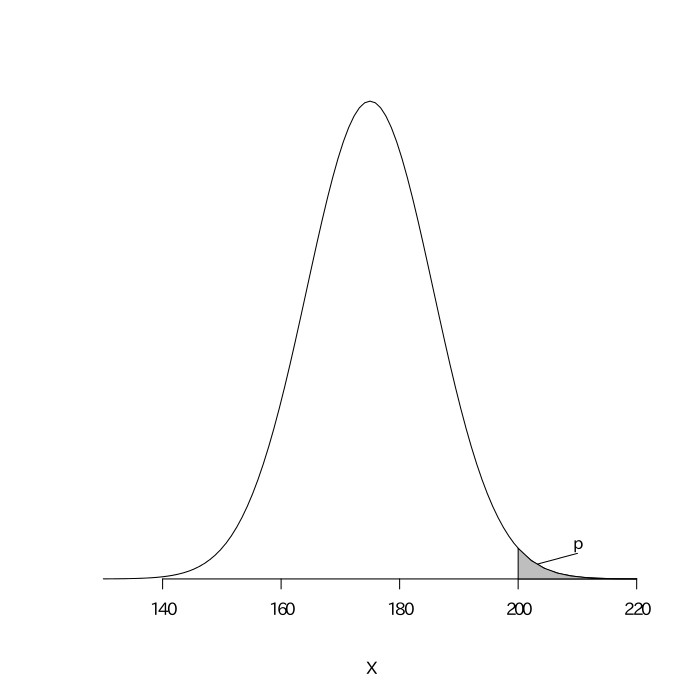
↓
【問題1】
次の図のように、0.36の割合で当たりとなるルーレットがある。500回このルーレットを回したときに、200回以上当たる確率を求めよ(標準正規分布表は与えられているものとする)。

(例題2)
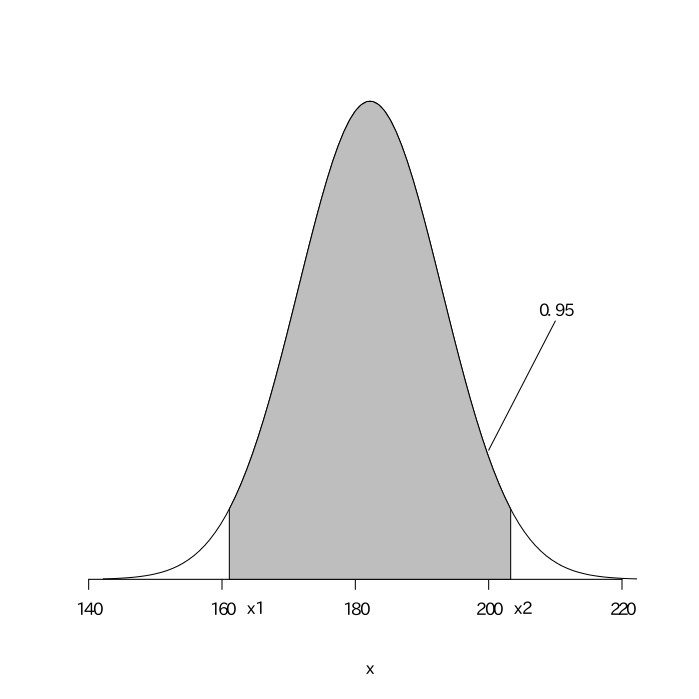
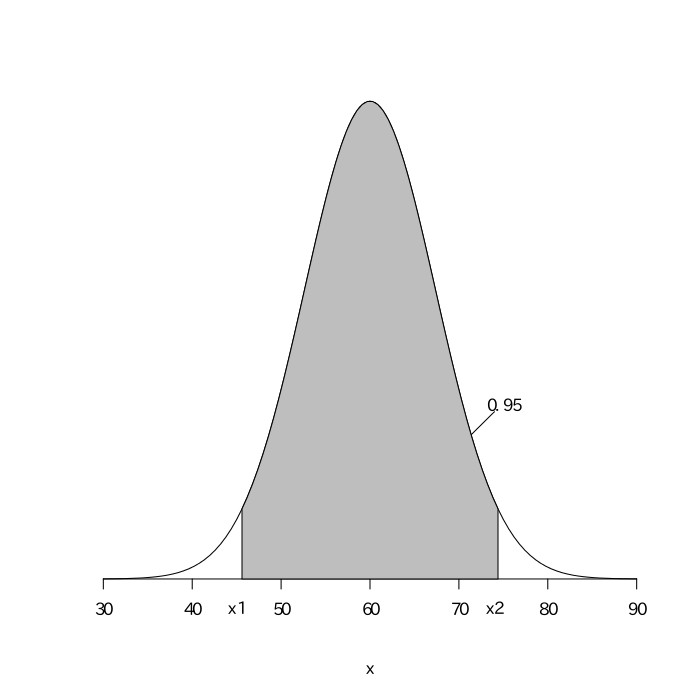
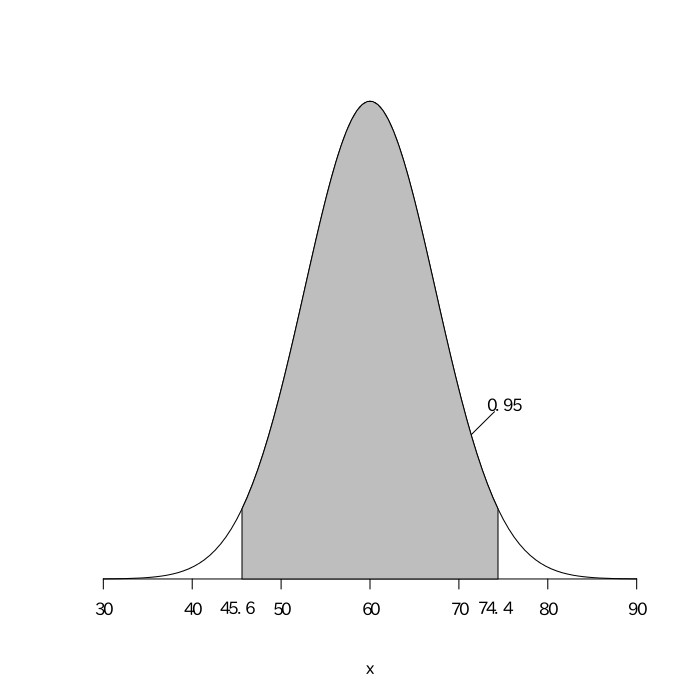
1994年にオリックスに在籍していたイチロー選手の打撃成績は、546打数210安打(.385)だった。このデータから、当時のイチロー選手の真の打率を、95%区間で推定せよ。
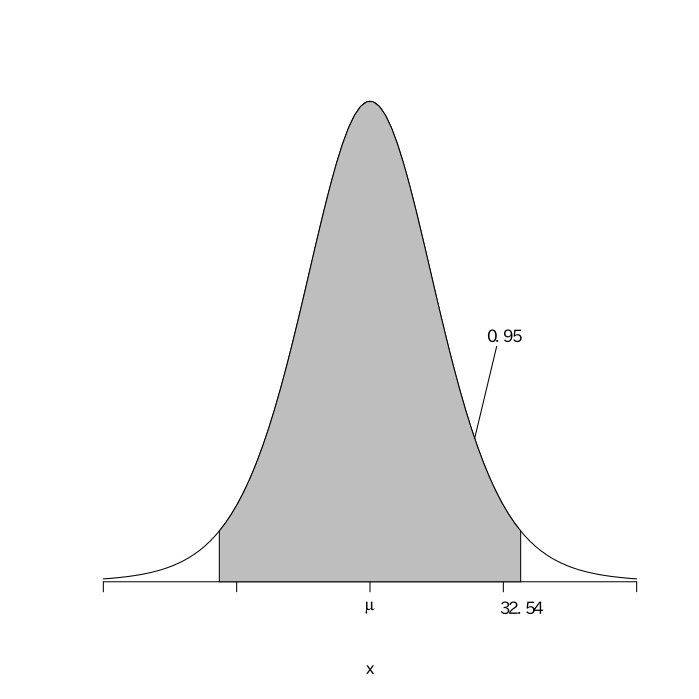
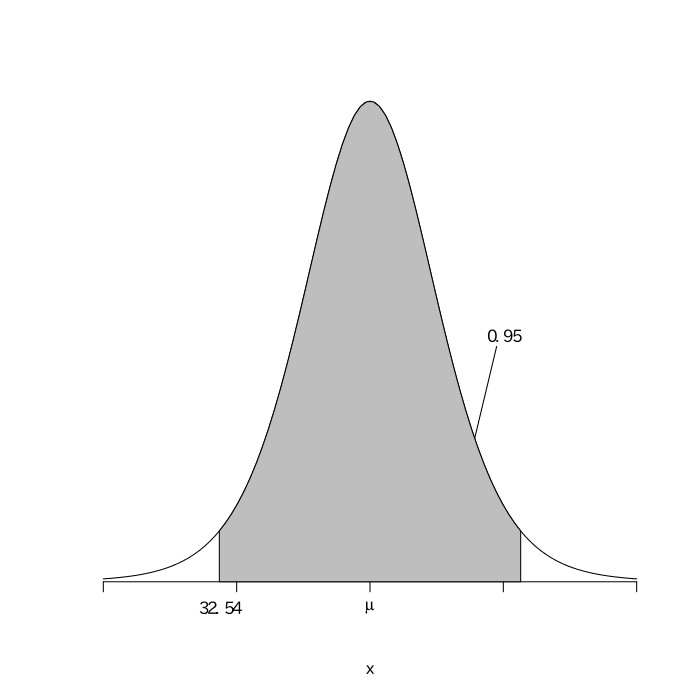
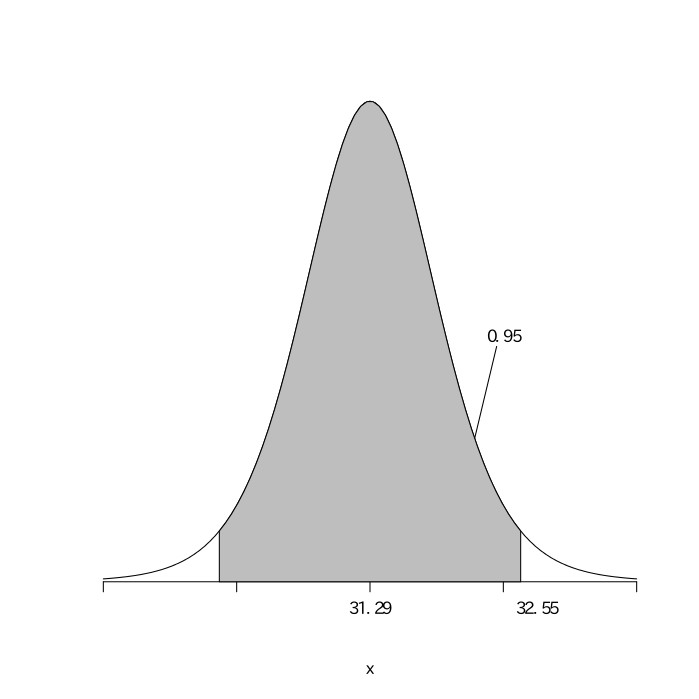
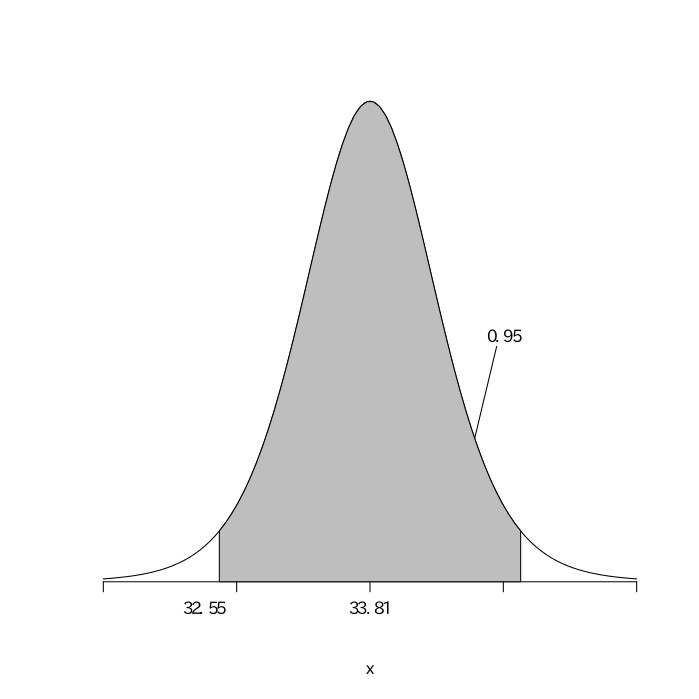
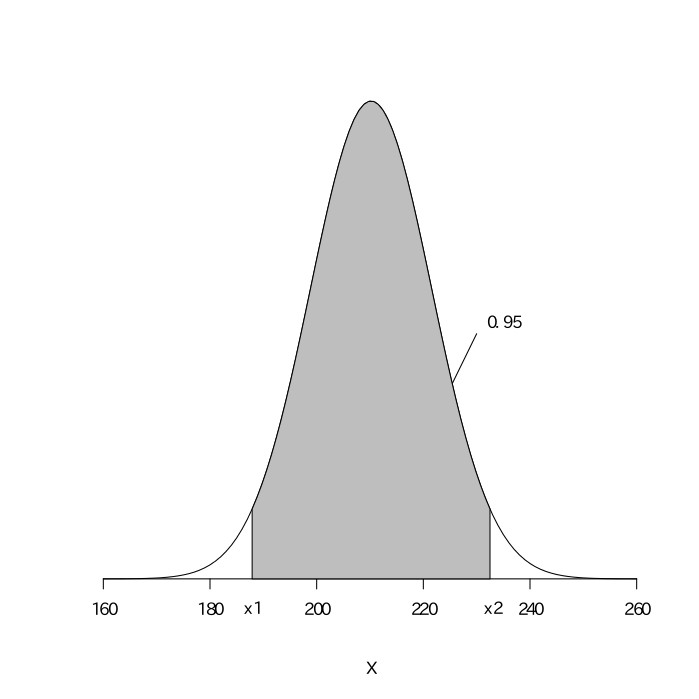
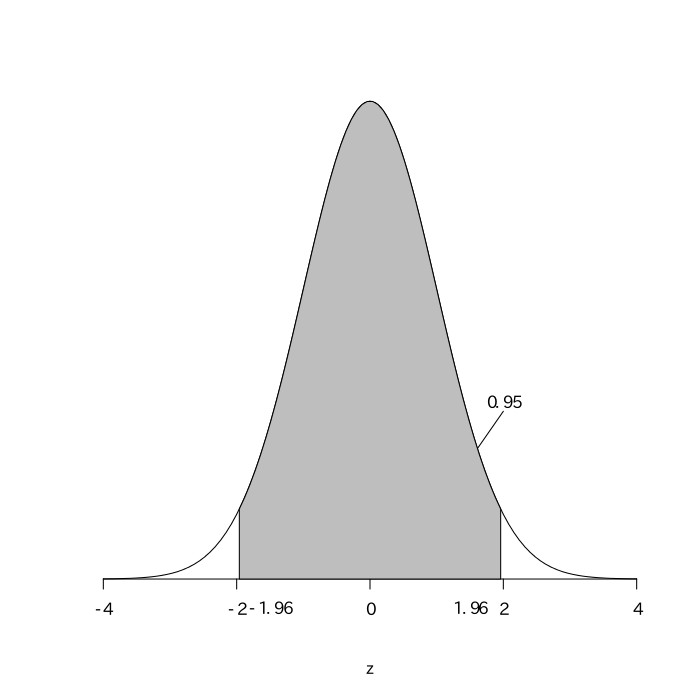
打数$(n)$が十分に大きいので、真の打率が$0.385$であると考える。真の打率を$0.385$として、$546$回の打数があるとすると、その安打数は$(546, 0.385)$の二項分布になるので、平均が$546\times0.385\fallingdotseq210.2$、分散が$210.2\times0.615\fallingdotseq129.3$の正規分布となる。安打数を$X$とすると、$\frac{X-210.2}{\sqrt{129.3}}$は平均が0、分散が1の標準正規分布になる。標準正規分布表から、$.4750$となる$z$の値を読み取ると$1.96$であることがわかる。よって、この標準正規分布における95%区間は、$-1.96\leqq\frac{X-210.2}{\sqrt{129.3}}\leqq1.96$となる。これを解くと$-1.96\leqq\frac{X-210.2}{11.37}\leqq1.96$
$-22.29\leqq{X-210.2}\leqq22.29$
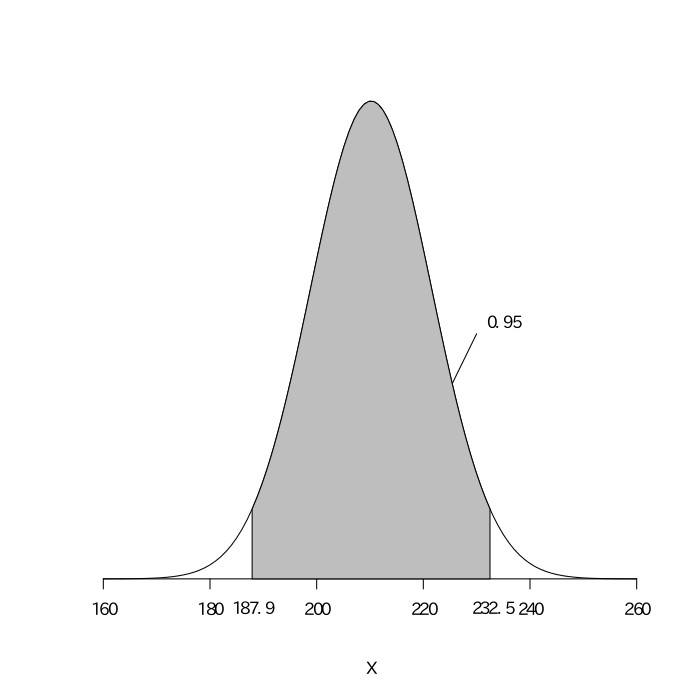
$187.9\leqq{X}\leqq232.5$
これを打数$(n)$で割ると
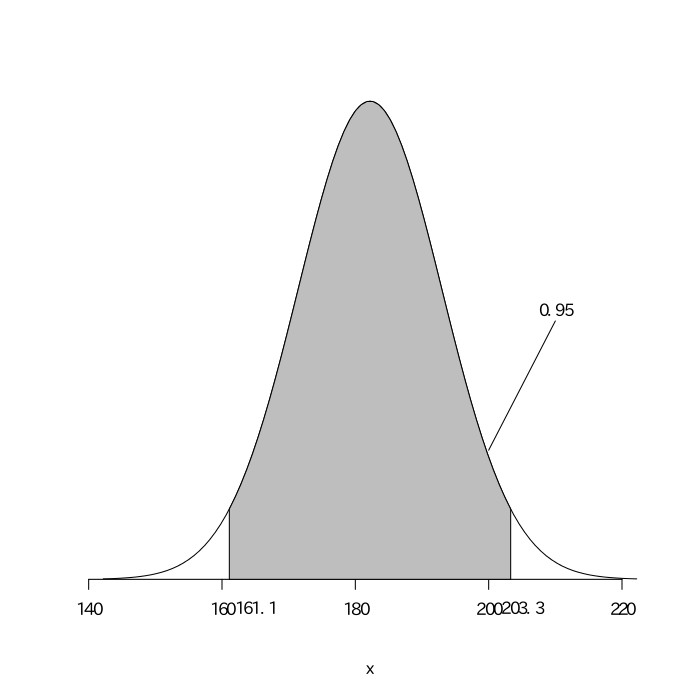
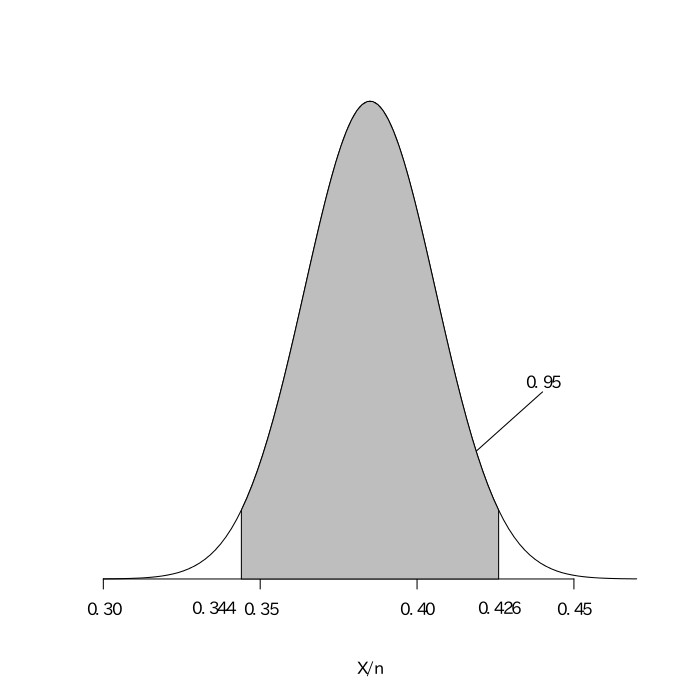
$0.344\leqq\frac{X}n\leqq0.426$
以上より、当時のイチロー選手の真の打率を95%区間で推定すると、.344以上、.426以下となる。
↓
↓
↓
【問題2】
2015年にソフトバンクに在籍していた柳田悠岐選手の打撃成績は、502打数182安打(.363)だった。このデータから、当時の柳田選手の真の打率を、95%区間で推定せよ。
(例題3)
1936年のアメリカ大統領選挙は、民主党のフランクリン・ルーズベルト候補と、共和党のアルフレッド・ランドン候補によって争われた。リテラリー・ダイジェスト誌は、自動車保有者と電話利用者の名簿を使って1千万人に調査をして、ランドン候補が当選すると予想したのに対し、ギャラップは、「収入中間層・都市居住者・女性」「収入下位層・農村部居住者・男性」のように互いに重ならないグループに分け、3000人を調査してルーズベルト候補が当選すると予想した。結果はルーズベルト候補が当選した。
1948年のアメリカ大統領選挙は、民主党のハリー・トルーマン候補と、共和党のトマス・デューイ候補によって争われた。ギャラップは1936年と同じ方法でデューイ候補が当選すると予想したが、結果はトルーマン候補が当選した。
それぞれの選挙に関して、どうしてそのような結果になったのかを考察せよ。
標本(調査対象者)が母集団(アメリカ大統領選挙の全有権者)をいかに適切に代表しているかという問題である。標本数よりも、標本が母集団からまんべんなく抜き取られていることが重要である。1948年のアメリカ大統領選挙は、民主党のハリー・トルーマン候補と、共和党のトマス・デューイ候補によって争われた。ギャラップは1936年と同じ方法でデューイ候補が当選すると予想したが、結果はトルーマン候補が当選した。
それぞれの選挙に関して、どうしてそのような結果になったのかを考察せよ。
1936年の大統領選挙に関しては、同時自動車や電話を保有していたのは裕福な人たちであり、それゆえ共和党支持者が多かったので、リテラリー・ダイジェスト誌が選んだ標本では母集団と比べて共和党支持者の比率が高かったために、誤った結論が導き出されたと考えられる。
1948年の大統領選挙に関しては、割り当てられた属性内での調査対象者が、調査員の主観によって選ばれていたために、ズレが生じたと考えられる。
現在では、こうした欠陥を克服するために、無作為抽出の方法がとられている。
【問題3】
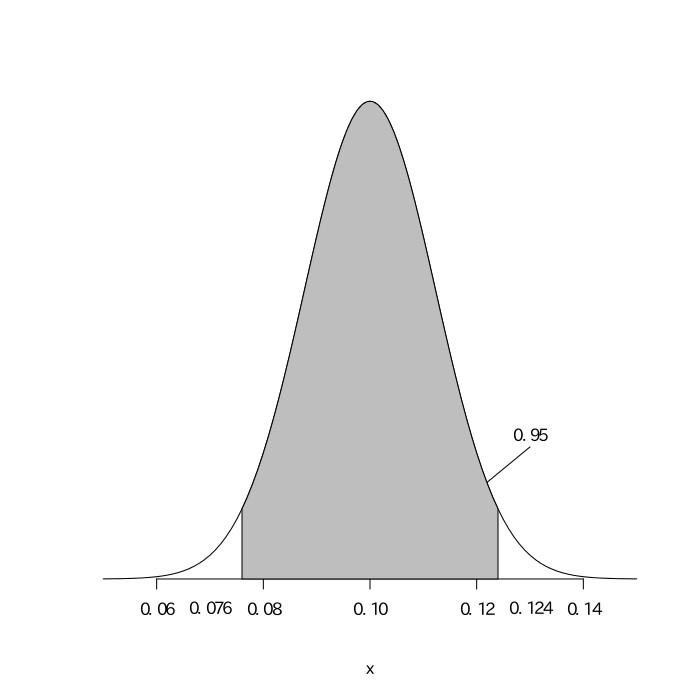
関東地方にはおよそ15,000,000世帯あるが、視聴率調査はそのうちの600世帯だけで行われている。視聴率が10%であったときの真の視聴率を95%区間で推定して、この調査が妥当かどうかを考えよ。
6.2 正規分布(大標本)
(例題4)
ある工業製品から50個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。この工業製品の平均重量を、信頼度95%の信頼区間で推定せよ。
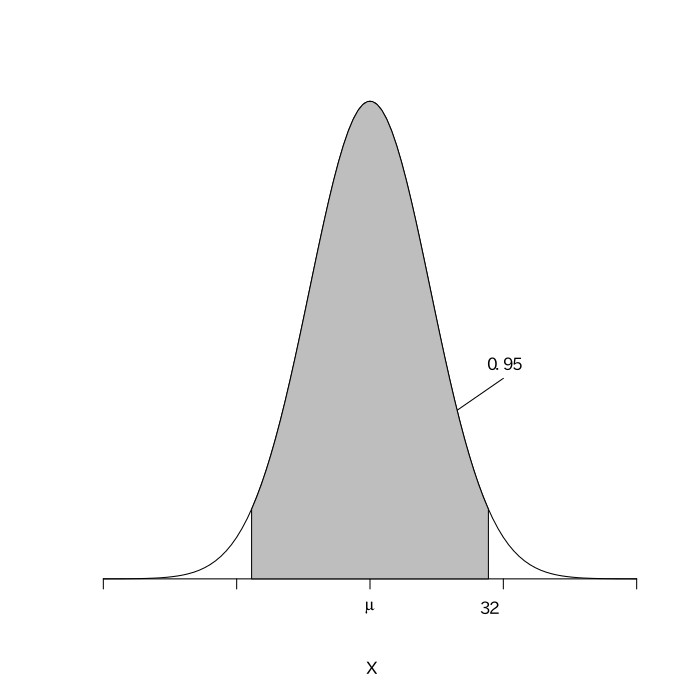
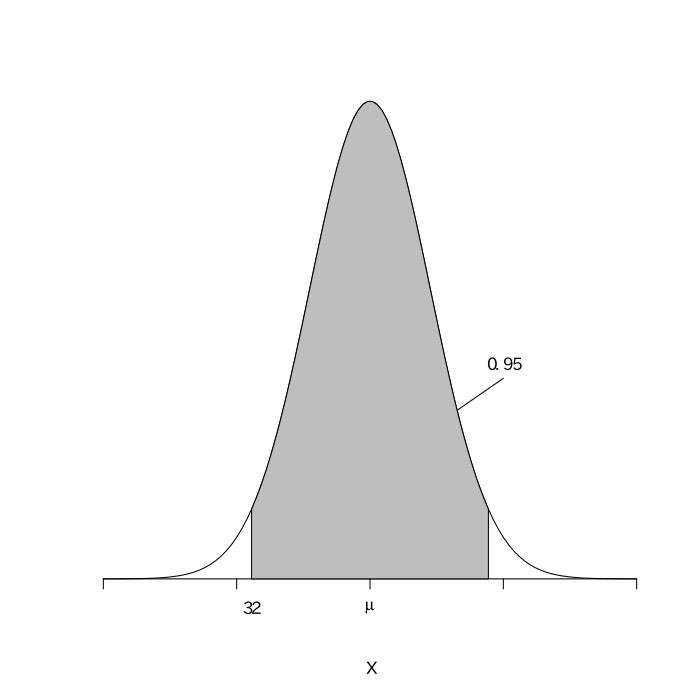
標本を何度も取ることを想定すると、標本平均の集合は、平均が母集団平均で分散が$\frac{母集団分散}{標本数}$の正規分布に従う(中心極限定理)。標本数が大きい場合は、母集団分散が標本分散に等しいと考えてもよい。本問では、標本数が50なので大きいと言える。${母集団平均}=\mu$とおく。${母集団分散}={標本分散}=10.24$と考える。標本平均の集合をXとすると、Xは平均が$\mu$、分散が$10.24\div50=0.2048$の正規分布に従い、$\frac{X-\mu}{\sqrt{0.2048}}$は平均が0、分散が1の標準正規分布になる。95%区間で推定をするので、標準正規分布表より、
$-1.96\leqq\frac{X-\mu}{\sqrt{0.2048}}\leqq1.96$
$-0.888\leqq{X-\mu}\leqq0.888$
$-0.888\leqq{-X+\mu}\leqq0.888$
$-0.888+X\leqq{\mu}\leqq0.888+X$
今、標本平均が32.0なので、これをXに代入すると
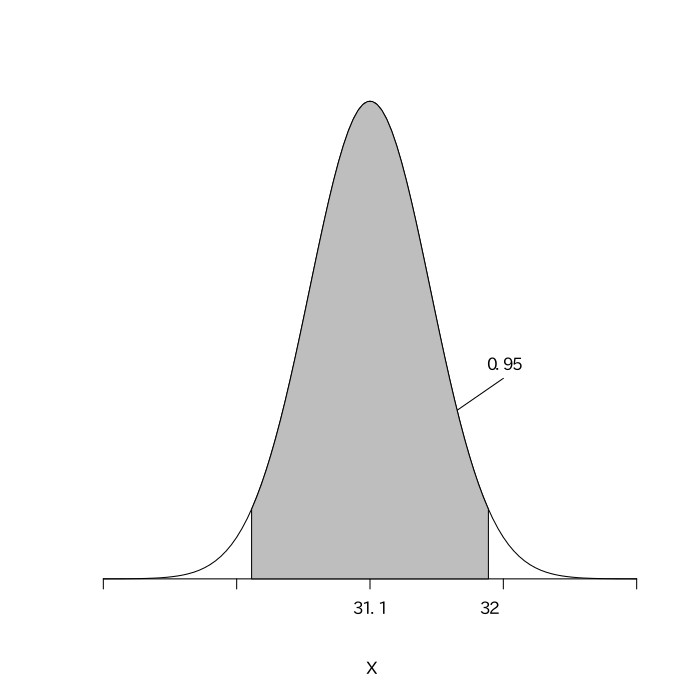
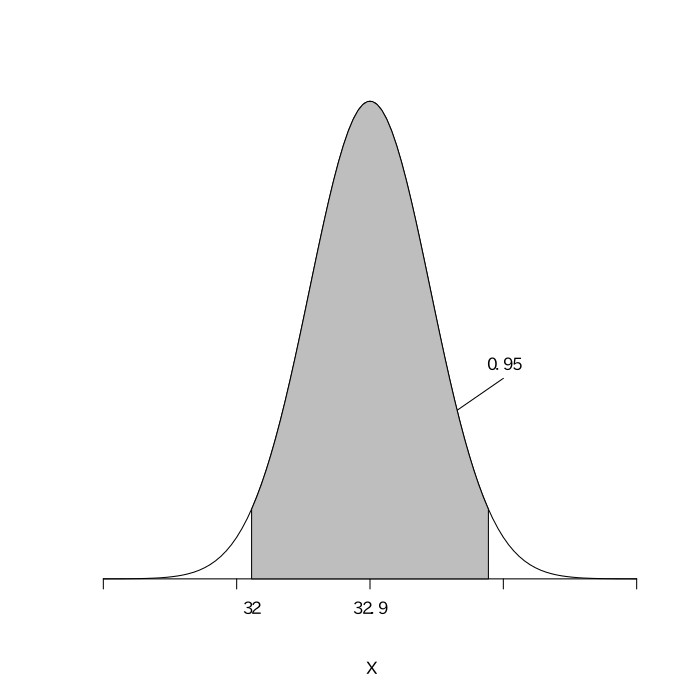
$31.112\leqq{\mu}\leqq32.888$
以上より、この工業製品の平均重量は、31.1g以上32.9g以下である。
↓

↓
【問題4】
ある怪しい男が両替屋に金貨を100枚持ってきた。その重さを測定すると、以下の通りであった。この金貨全体の平均重量を95%区間で推定せよ。
| 29.92 | 27.73 | 31.34 | 31.67 | 37.04 | 33.86 | 30.08 | 31.94 | 24.20 | 30.08 |
| 28.37 | 32.75 | 29.18 | 29.39 | 35.59 | 32.79 | 27.92 | 36.20 | 32.81 | 30.69 |
| 32.27 | 30.24 | 33.63 | 33.20 | 26.58 | 34.38 | 27.72 | 31.43 | 29.88 | 25.33 |
| 30.94 | 31.36 | 28.56 | 28.94 | 28.63 | 29.18 | 26.54 | 30.85 | 35.31 | 31.19 |
| 31.86 | 28.29 | 31.18 | 31.92 | 27.79 | 34.33 | 34.88 | 34.53 | 29.26 | 28.24 |
| 31.00 | 28.43 | 35.75 | 34.73 | 32.99 | 29.29 | 31.93 | 30.76 | 34.89 | 33.63 |
| 29.85 | 30.78 | 30.49 | 34.20 | 27.25 | 32.34 | 29.09 | 29.36 | 31.78 | 31.45 |
| 29.95 | 32.59 | 33.23 | 27.99 | 32.67 | 35.32 | 31.37 | 31.11 | 26.80 | 24.9 |
| 32.20 | 29.80 | 30.85 | 36.41 | 36.68 | 28.61 | 33.25 | 28.78 | 33.75 | 37.31 |
| 29.65 | 31.45 | 29.29 | 34.15 | 30.87 | 30.88 | 32.53 | 31.29 | 32.90 | 27.81 |
6.3 t分布(小標本)
(例題5)
ある工業製品から10個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。ただし、この工業製品の重量は正規分布しているとする。この工業製品の平均重量を、信頼度95%の信頼区間で推定せよ。
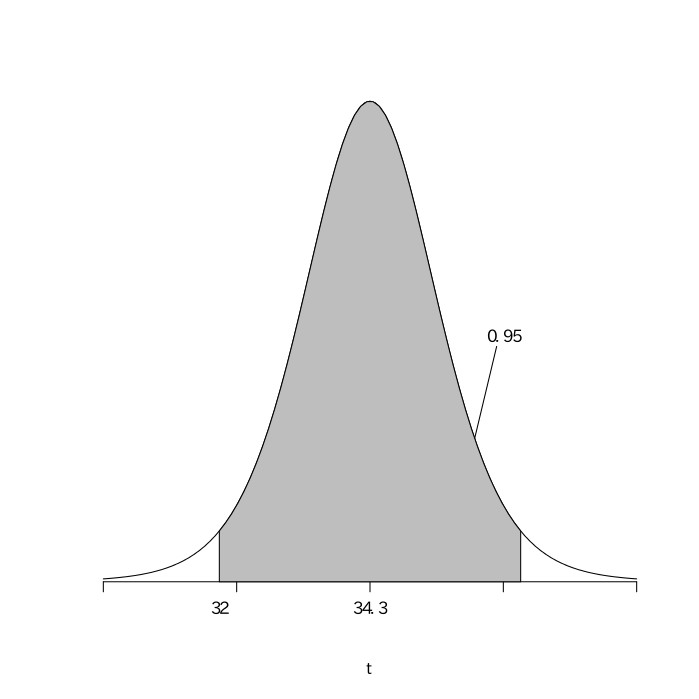
標本を何度も取り、標本平均の集合を考えると、母集団が正規分布している場合、平均が母集団平均で分散が$\frac{母集団分散}{標本数}$の正規分布に従う。標本数が小さい場合は、母集団分散が標本分散に等しいと考えてはならない。本問では、標本数が10なので大きいと言えない。${母集団平均}=\mu$とおく。標本平均の集合をXとすると、Xは平均が$\mu$、分散が${母集団分散}\div10$の正規分布に従い、$\frac{X-\mu}{\sqrt{{母集団分散}\div10}}$は平均が0、分散が1の標準正規分布になる。この式の母集団分散の代わりに標本分散を用いた$T=\frac{X-\mu}{\sqrt{{標本分散}\div10}}=\frac{X-\mu}{\sqrt{1.024}}$は、正規分布ではなく、自由度が$10{(標本数)}-1=9$のt分布に従うことがわかっている(正確には標本分散ではなく、標本分散を$\frac{n}{n-1}$倍した不偏分散を用いるが、ここでは簡略化のため標本分散で代用した)。
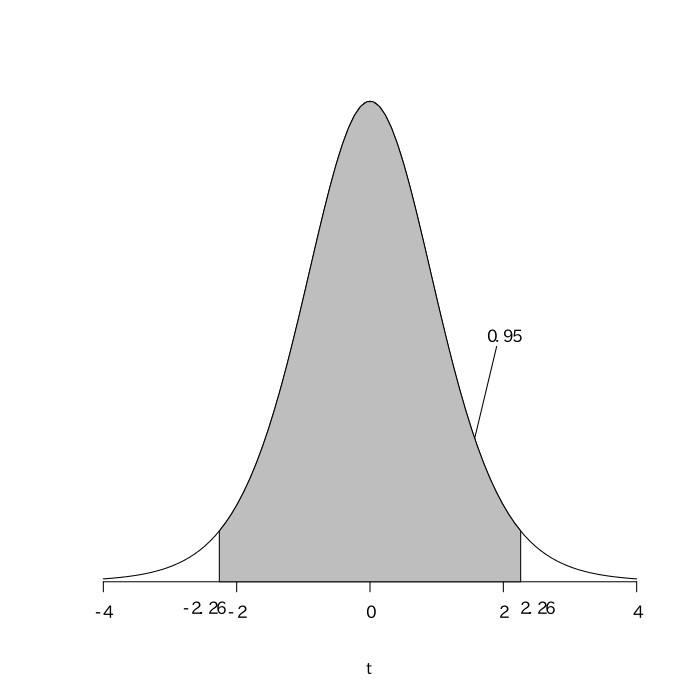
95%区間で推定をするので、t分布表より、
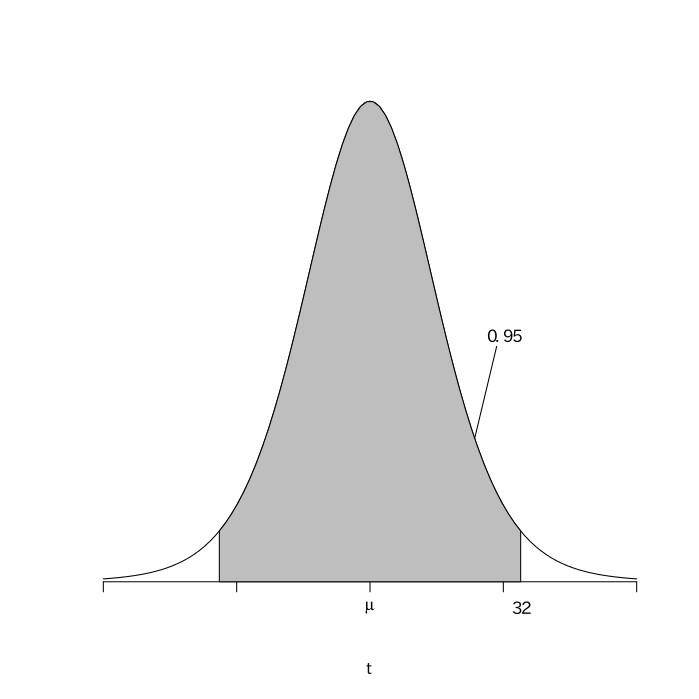
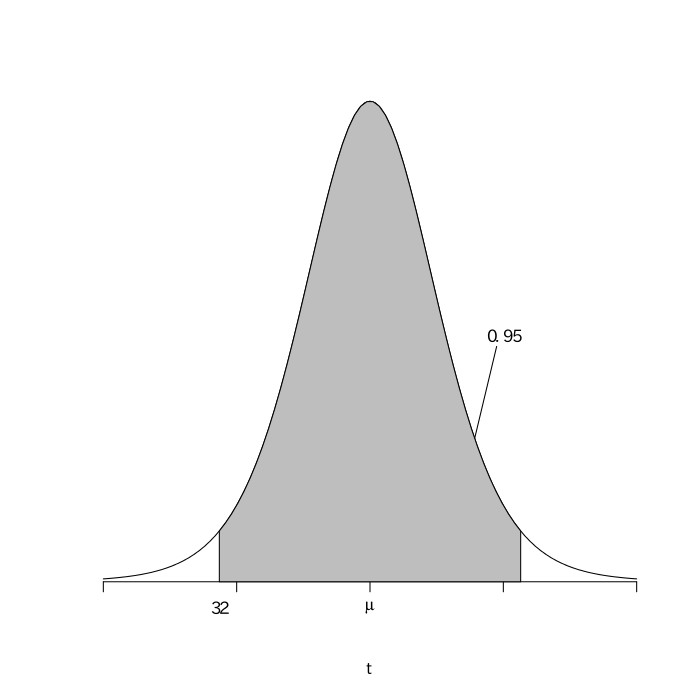
$-2.26\leqq\frac{X-\mu}{\sqrt{1.024}}\leqq2.26$
$-2.287\leqq{X-\mu}\leqq2.287$
$-2.287\leqq{-X+\mu}\leqq2.287$
$-2.287+X\leqq{\mu}\leqq2.287+X$
今、標本平均が32.0なので、これをXに代入すると
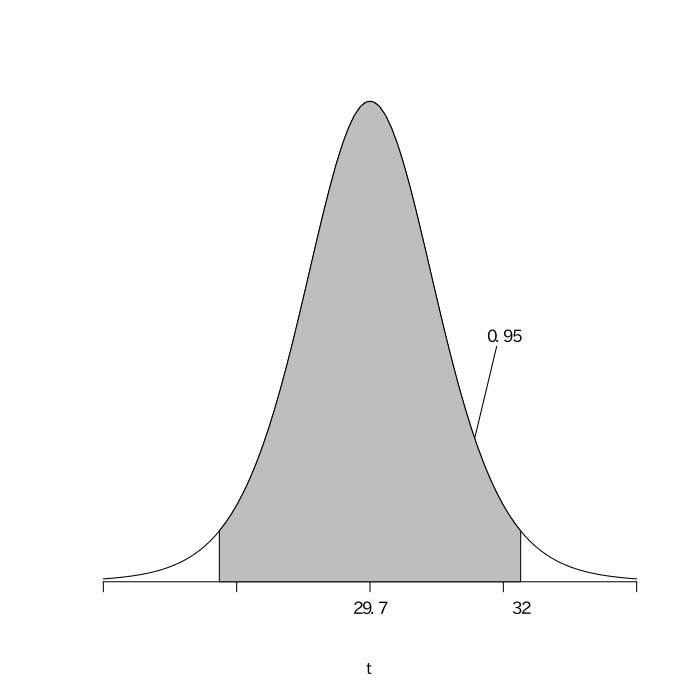
$29.713\leqq{\mu}\leqq34.287$
以上より、この工業製品の平均重量は、29.7g以上34.3g以下である。
↓
↓
【問題5】
ある怪しい男が両替屋に金貨を10枚持ってきた。その重さを測定すると、以下の通りであった。ただし、この金貨全体の重量は正規分布しているとする。この金貨全体の平均重量を95%区間で推定せよ。
| 31.36 | 34.33 | 29.18 | 32.81 | 34.15 | 32.75 | 35.31 | 33.23 | 31.67 | 30.69 |
6.4 $\chi^2$分布
(例題6)
ある工業製品から10個を無作為抽出して重量を調査したとき、その標本の平均重量は32.0g、その標本の標準偏差は3.2gであった。ただし、この工業製品の重量は正規分布しているとする。この工業製品の重量の分散を、信頼度95%の信頼区間で推定せよ。
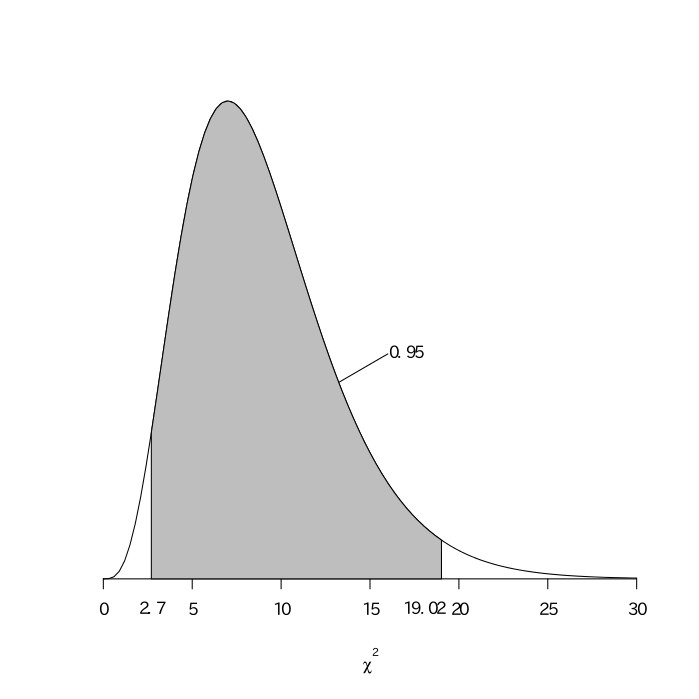
平均が$\mu$、分散が$\sigma^2$の正規分布からランダムに取り出した標本を$x_1, x_2, x_3, \cdots, x_n$として、そのそれぞれと平均との差を標準偏差で割って標準化したものの2乗の和$(\frac{x_1-\mu}{\sigma})^2+(\frac{x_2-\mu}{\sigma})^2+(\frac{x_3-\mu}{\sigma})^2+\cdots+(\frac{x_n-\mu}{\sigma})^2$は、自由度が$n$の$\chi^2$分布に従うことが知られている。$\mu$の代わりに標本平均$\bar{x}$を用いた$(\frac{x_1-\bar{x}}{\sigma})^2+(\frac{x_2-\bar{x}}{\sigma})^2+(\frac{x_3-\bar{x}}{\sigma})^2+\cdots+(\frac{x_n-\bar{x}}{\sigma})^2$は、自由度が$n-1$の$\chi^2$分布に従う。標本分散を$s^2$とすると、$s^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+(x_3-\bar{x})^2+\cdots+(x_n-\bar{x})^2}{n}$より、$(x_1-\bar{x})^2+(x_2-\bar{x})^2+(x_3-\bar{x})^2+\cdots+(x_n-\bar{x})^2=ns^2$となるので、$\frac{ns^2}{\sigma^2}$が自由度が$n-1$の$\chi^2$分布に従うとも言える。本問では、$n=10, s^2=10.24$なので、$\frac{102.4}{\sigma^2}$が自由度が$9$の$\chi^2$分布に従う。
$\chi^2$分布表より自由度が$9$の値を読むと、$p=0.975$が2.70、$p=0.025$が19.02なので、$2.70\leqq\frac{102.4}{\sigma^2}\leqq19.02$を考えればよい。
(ア)
$2.70\leqq\frac{102.4}{\sigma^2}$より
$2.70{\sigma^2}\leqq102.4$
${\sigma^2}\leqq37.93$
(イ)
$\frac{102.4}{\sigma^2}\leqq19.02$より
$102.4\leqq19.02\sigma^2$より
$5.39\leqq\sigma^2$
以上より、この工業製品の重量の分散は、5.4以上37.9以下であると推定できる。
【問題6】
ある怪しい男が両替屋に金貨を10枚持ってきた。その重さを測定すると、以下の通りであった。ただし、この金貨全体の重量は正規分布しているとする。この金貨全体の重量の分散を95%区間で推定せよ。
| 31.36 | 34.33 | 29.18 | 32.81 | 34.15 | 32.75 | 35.31 | 33.23 | 31.67 | 30.69 |