第3章 確率
3.1 確率の定義
ある事象が同様に確からしいときに、確率は、$\frac{ある事象の総数}{全事象の総数}$で求めることができる。(例題1)
1つのサイコロを投げた時に、5以上の目が出る確率はいくらか。
全事象の総数は1, 2, 3, 4, 5, 6の6通り。5以上の目が出る総数は5, 6の2通り。よって$\frac{2}{6}=\frac{1}{3}$* 確率の定義からして、確率をPとすると、$0\leqq{P}\leqq1$である。
【問題1】
コインを2枚投げた時、表が1枚、裏が1枚出る確率を求めたい。次のAさんとBさんのどちらの求め方が正しいか。
Aさん:全事象の総数は、表が2枚、表が1枚で裏が1枚、裏が2枚の3通り。表が1枚で裏が1枚の総数は1通り。よって$\frac13$。
Bさん:全事象の総数は、(表、表)、(表、裏)、(裏、表)、(裏、裏)の4通り。表が1枚で裏が1枚の総数は2通り。よって$\frac24=\frac12$
Aさん:全事象の総数は、表が2枚、表が1枚で裏が1枚、裏が2枚の3通り。表が1枚で裏が1枚の総数は1通り。よって$\frac13$。
Bさん:全事象の総数は、(表、表)、(表、裏)、(裏、表)、(裏、裏)の4通り。表が1枚で裏が1枚の総数は2通り。よって$\frac24=\frac12$
【問題2】
今日は日本プロ野球のシーズン最終戦、9回裏2アウト満塁である。前日までの打率が.350のあるバッターが本日5回目の打席に入った。それまでの4打席は凡退している。そのときのコメントとして、次のどの解説者が正しいと思われるか。
A : 「このバッターの打率は.350なので0.35の確率でヒットを打つ」
B : 「このバッターが5打席連続で凡退するとは考えにくいから、0.35よりも高い確率でヒットを打つ」
C : 「4打席連続で凡退しているということは今日は調子が悪いのだから、ヒットを打つ確率は0.35よりも低い。」
A : 「このバッターの打率は.350なので0.35の確率でヒットを打つ」
B : 「このバッターが5打席連続で凡退するとは考えにくいから、0.35よりも高い確率でヒットを打つ」
C : 「4打席連続で凡退しているということは今日は調子が悪いのだから、ヒットを打つ確率は0.35よりも低い。」
(例題2)
8 本のくじの中に 2 本当たりくじが入っている。この 8 本のくじから A 君が 1 本ひき、これをもとに戻さな
いで、B 君がもう 1 本ひくとき、どちらが当たりやすいか。
A君が当たる確率は$\frac28=\frac14$A君が当たってB君も当たる確率は$\frac28\times\frac17=\frac1{28}$
A君がはずれてB君が当たる確率は$\frac68\times\frac27=\frac6{28}$
B君が当たる確率は$\frac1{28}+\frac6{28}=\frac7{28}=\frac14$
以上より、当たりやすさは同じである。
【問題3】
4 本の当たりくじを含む 10 本のくじがある。A, B がこの順にこのくじを 1 本ずつ引く。ただし、引いたく
じはもとに戻さない。このとき、このときどちらが当たりやすいか。
3.2 条件付き確率
(例題3)
5回に1回の割合で帽子を忘れるくせのあるK君が、正月に A、B、C 3軒を順に年始回りをして家に帰ったとき、帽子を忘れてきたことに気がついた。2軒目の家 B に忘れてきた確率を求めよ。(早稲田大学の入試問題より)
A, B, Cと順番に回っているのでCよりもB、BよりもAで忘れる確率が高い(Aで帽子を忘れるともうBやCで忘れることはできない)ので、$\frac13$とは限らない。また、Bに来た時点で帽子をすでに忘れてきたかもしれないので、$\frac15$というわけでもない。
さらに、Aで帽子を忘れずにBで帽子を忘れるので$\frac45\times\frac15=\frac4{25}$と考えたとしても、これはどの家でも帽子を忘れない事象を無視しているので、誤っている。
正しくは
- Aで忘れる確率
$\frac15$ - Bで忘れる確率
$\frac45\times\frac15=\frac4{25}$ - Cで忘れる確率
$\frac45\times\frac45\times\frac15=\frac{16}{125}$ - A, B, Cのどこかで帽子を忘れる確率
$\frac15+\frac4{25}+\frac{16}{125}=\frac{61}{125}$ - どこかで帽子を忘れてきたと気づいたときに、忘れたのがBであった確率(求める確率)
$\frac{\frac4{25}}{\frac{61}{125}}=\frac{20}{61}$
【問題4】
区別のつかない3つの箱があり、その中に1個だけ、当たりくじの入っている箱がある。解答者は、まず1つの箱を選ぶ。司会者は、どの箱に当たりくじが入っているかを知っているので、残った2つの箱から当たりくじの入っていない箱を1個だけ取り除く。そこで、解答者は司会者から、選んだ箱を変えるチャンスを与えられる。解答者は箱を変えたほうがいいか、それともそのままのほうがいいか。
(例題4)
ある感染症は1万人に1人の割合で感染していることがわかっている。この感染症の検査は99%の精度である(この感染症に感染している人がこの検査を受けると99%の確率で陽性の結果が出る)。Aさんがこの感染症の検査をして「陽性」と出たときに、Aさんがこの感染症に感染している確率はいくらか。
1万人に1人だから0.0001だということにはならない(それだと検査をした意味がない)。陽性の結果が出たからといって99%で感染しているとは限らない(逆は必ずしも真ならず)
- Aさんが感染していて陽性の結果が出る確率
$\frac1{10000}\times\frac{99}{100}=\frac{99}{1000000}$ - Aさんが感染しておらず陽性の結果が出る確率
$\frac{9999}{10000}\times\frac{1}{100}=\frac{9999}{1000000}$ - 陽性の結果が出る全体の確率
$\frac{99}{1000000}+\frac{9999}{1000000}=\frac{10098}{1000000}$ - 陽性の結果が出たときにAさんが感染している確率(求める確率)
$\frac{\frac{99}{1000000}}{\frac{10098}{1000000}}=\frac{99}{10098}=\frac{1}{102}$(約1%)
【問題5】
ある工場で、製品が規格内である確率が、0.9であるとする。製品を検査するとき、規格内の製品は、確率0.95で合格と判定され、規格外の製品は、確率0.15で合格と判定されるという。いま、一つの製品が、この検査で2度合格と判定されたとき、この製品が規格内の製品である確率を求めよ。
3.3 余事象の確率
(例題5)
40人のクラスで同じ誕生日の人がいる確率を求めよ(閏年は考えないものとする)。
求める確率は$1-$同じ誕生日の人がいない確率である。同じ誕生日の人がいない確率は$1\times\frac{364}{365}\times\frac{363}{365}\times\frac{362}{365}\times...\times\frac{326}{365}\fallingdotseq0.109$
以上より求める確率は、$1-0.109=0.891$より、約0.891(89.1%)
【問題6】
サイコロを5回投げて少なくとも1回は奇数の目が出る確率を求めよ。
3.4 二項定理
(例題6)
ア〜エの4つの選択肢の中から1つを選んで答える6 題の問題にでたらめに回答するときに、5問以上正解する確率を求めよ。
- 6問正解する
$(\frac14)^6=\frac1{4096}$ - 5問正解する
5問正解するのは、正解する問題番号に着目すると、次の6通りある。
そのそれぞれの確率は$(\frac14)^5\times\frac34=\frac3{4096}$なので、5問正解する確率は$\frac3{4096}\times6=\frac{18}{4096}$(1) (2) (3) (4) (5) (6) ◯ ◯ ◯ ◯ ◯ × ◯ ◯ ◯ ◯ × ◯ ◯ ◯ ◯ × ◯ ◯ ◯ ◯ × ◯ ◯ ◯ ◯ × ◯ ◯ ◯ ◯ × ◯ ◯ ◯ ◯ ◯ - 結論
以上より、求める確率は、$\frac{1}{4096}+\frac{18}{4096}=\frac{19}{4096}$
【問題7】
ア〜エの4つの選択肢の中から1つを選んで答える6 題の問題にでたらめに回答するときに、4問以上正解する確率を求めよ。
3.5 確率分布
(例題7)
平成26年12月31日に抽選が行われた第669回全国自治宝くじ(年末ジャンボ)の結果は次の通りであった。なお、この宝くじは100000番から199999番までの10万枚を1組、01組から100組までの100組の合計10万×100=1000万枚を1ユニットとして販売されている。
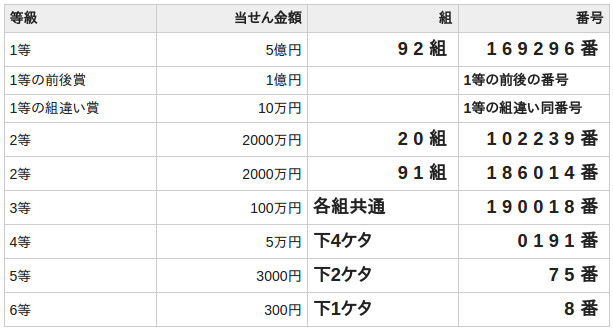
(出典:みずほ銀行 宝くじコーナー:第669回全国自治宝くじ(年末ジャンボ)
http://www.mizuhobank.co.jp/takarakuji/tsujyo/jumbo/0669.html
この宝くじを1枚買ったときに得られる金額の期待値を求めよ。
1ユニットあたり、1等は1本、1等の前後賞は2本、1等の組違い賞は99本、2等は2本、3等は100本、4等は1000本、5等は100000本、6等は1000000本である。獲得金額をX、その確率をPとして、確率分布表をかく。

(出典:みずほ銀行 宝くじコーナー:第669回全国自治宝くじ(年末ジャンボ)
http://www.mizuhobank.co.jp/takarakuji/tsujyo/jumbo/0669.html
この宝くじを1枚買ったときに得られる金額の期待値を求めよ。
| X | 5億 | 1億 | 10万 | 2000万 | 100万 | 5万 | 3,000 | 300 |
| P | $\frac{1}{10000000}$ | $\frac{2}{10000000}$ | $\frac{99}{10000000}$ | $\frac{2}{10000000}$ | $\frac{100}{10000000}$ | $\frac{1000}{10000000}$ | $\frac{100000}{10000000}$ | $\frac{1000000}{10000000}$ |
$500,000,000\times\frac{1}{10000000}$
$+100,000,000\times\frac{2}{10000000}$
$+100,000\times\frac{99}{10000000}$
$+20,000,000\times\frac{2}{10000000}$
$+1,000,000\times\frac{100}{10000000}$
$+50,000\times\frac{1000}{10000000}$
$+3,000\times\frac{100000}{10000000}$
$+300\times\frac{1000000}{10000000}$
$=\frac{1499900000}{10000000}=149.99$円
【問題8】
平成26年12月31日に抽選が行われた第670回全国自治宝くじ(年末ジャンボミニ7000万)の結果は次の通りであった。なお、この宝くじは100000番から199999番までの10万枚を1組、01組から100組までの100組の合計10万×100=1000万枚を1ユニットとして販売されている。
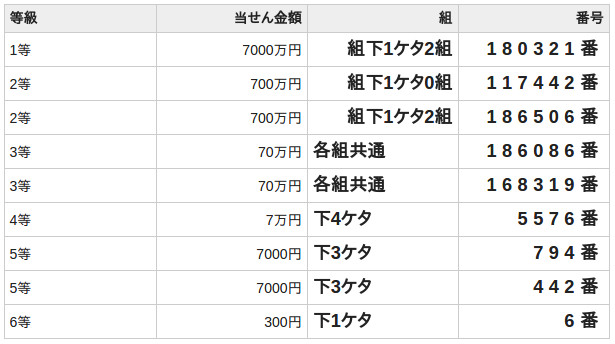
(出典:みずほ銀行 宝くじコーナー:第670回全国自治宝くじ(年末ジャンボミニ7000万)
http://www.mizuhobank.co.jp/takarakuji/tsujyo/jumbo/0670.html
この宝くじを1枚買ったときに得られる金額の期待値を求めよ。

(出典:みずほ銀行 宝くじコーナー:第670回全国自治宝くじ(年末ジャンボミニ7000万)
http://www.mizuhobank.co.jp/takarakuji/tsujyo/jumbo/0670.html
この宝くじを1枚買ったときに得られる金額の期待値を求めよ。
(例題8)
甲乙二人がおのおの32ピストル(当時のお金の単位)の金を賭けて勝負したとする。そしてどちらかが先に3点を得たものを勝ちとし、勝った方がかけ金の総額64ピストルをもらえるとする。ところが甲が2点、乙が1点を得たとき、勝負が中止になってしまった。このとき、二人のかけ金の総額64ピストルを甲と乙にどのように分配すればよいだろうか。ただし二人の力は互角で、勝つ確率はそれぞれ1/2ずつだとする。
(パスカルとフェルマーの書簡より)
(パスカルとフェルマーの書簡より)
(ア)パスカルの解答
- 次に甲が得点する場合
次に甲が得点する場合は、甲が3点を得て勝つので、甲が64ピストルをもらえる。 - 次に乙が得点する場合
次に乙が得点する場合は、甲と乙が同点になるので、賭け金を半分ずつ分配して、甲が32ピストル、乙が32ピストルもらえる。 - 結論
次に甲が得点するか乙が得点するかは半々の確率なので、甲は、$64\times\frac12+32\times\frac12=48$ピストル、乙は16ピストルもらえるように分配するとよい。
* パスカルは神の存在について期待値を考えている。神が存在するほうに賭けて神が存在した場合の利得は無限大であるのに対し、神が存在しないほうに賭けた場合の利得(マイナスを含む)は有限なので、神が存在するほうに賭ける期待値は無限大となり、そちらに賭けるべきだという結論になる。
(イ)フェルマーの解答
得点の機会が5回あれば必ず決着する。そこで、途中で勝負が決着するとしないとにかかわらず、あと2回の試行を行うと考える。そうすると、その得点のあり方は(甲、甲)、(甲、乙)、(乙、甲)、(乙、乙)の4通りである。このうち甲が勝利するのは3通り、乙が勝利するのは1通りなので、総額64ピストルを甲:乙=3:1になるように分配して、甲が48ピストル、乙が16ピストルとなるように分配すればよい。
(ウ)確率分布による解答
- 甲が3勝1敗で勝利する確率
次の回で甲が得点する確率なので、$\frac12$である - 甲が3勝2敗で勝利する確率
次の回で乙が得点して、その次の回で甲が得点する確率なので、$\frac12\times\frac12=\frac14$ - 甲が勝利する確率
(1), (2)より甲が勝利する確率は$\frac12+\frac14=\frac34$
| X | 64 | 0 |
| P | $\frac34$ | $\frac14$ |
【問題9】
現在、日本プロ野球では、シーズン1位のチームが自動的に日本シリーズに進出するのではなく、クライマックスシリーズファイナルでシーズン2位または3位のチームと対戦し、先に4勝しなければ日本シリーズに進出できない。ただし、シーズン1位のチームにはクライマックスシリーズファイナルでアドバンテージの1勝が与えられている。そして日本シリーズに進出すると、興行収入で5億円の収入が見込まれるという。このとき、リーグ優勝を決めた時点で、あるチームが日本シリーズの興行収入として得られる収入の期待値を求めよ。ただし、どのチームの勝つ確率も$\frac12$であるとする。
作成:浅野直樹

このサイトの内容は、クレジットを表示し、それをもとに作成された新しい作品が元の作品と同様の条件で提供される限りは、改変や商用利用も含めてご自由にお使いいただけます。
記載が不正確であったことなどにより損害が生じた場合の責任は負いません。
間違いなどを発見した場合はお問い合わせからお知らせいただけるとありがたいです。